Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Lines and Angles

Short Answer Type

71. In figure, find the value of x.

140 Views

72. In figure, if QT ⊥ PR, ∠TQR = 40° and ∠SPR = 30°, find the value of x and y.

183 Views

73. In figure, if line segment AB intersects CD at O such that ∠OAD = 80°, ∠ODA = 50° and ∠OCB = 40°, then find ∠OBC.

268 Views

74. In figure, AP and DP are bisectors of two adjacent angles A and D of a quadrilateral ABCD. Prove that 2 ∠APD = ∠B + ∠C.

4620 Views

75. In figure, AB II DE, ∠ABC = 75°, ∠CDE = 145°, find ∠BCD.

362 Views

76. In figure, the side BC of ∆ABC is produced to D. The bisector of ∠A meets BC in L. Prove that ∠ABC + ∠ACD = 2 ∠ALC

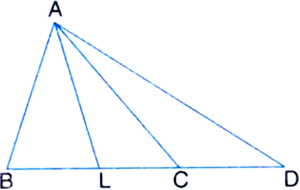
Given: The side BC of ∆ABC is produced to D. The bisector of ∠A meets BC in L.
To Prove: ∠ABC + ∠ACD = 2 ∠ALC.
Proof: ∠ABC + ∠ACD
= ∠ABC + (∠ABC + ∠BAC)
| Exterior angle theorem
= 2 ∠ABC + ∠BAC
= 2 ∠ABC + 2 ∠BAL
| ∵ AL is the bisector of ∠A
= 2 (∠ABC + ∠BAL)
= 2 ∠ALC | Exterior angle theorem

341 Views