 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type Short Answer Type
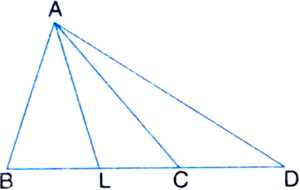
Short Answer TypeGiven: ABC is a triangle right angled at A. AL is drawn perpendicular to BC.
To Prove: ∠BAL = ∠ACB
Proof: In triangle ALB,
∠ALB + ∠BAL + ∠ABL = 180°
| Angle sum property of a triangle
⇒ 90° + ∠BAL + ∠ABC = 180°
⇒ ∠BAL + ∠ABC = 90° ...(1)
In triangle ABC,
∠BAC + ∠ACB + ∠ABC = 180°
| Angle sum property of a triangle
⇒ 90° + ∠ACB + ∠ABC = 180°
⇒ ∠ACB + ∠ABC = 90° ...(2)
From (1) and (2),
∠BAL + ∠ABC = ∠ACB + ∠ABC
⇒ ∠BAL = ∠ACB
