Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Lines and Angles

Short Answer Type

81. In figure, the side BC of a ∆ABC is produced to D. The bisector of ∠BAC intersects the side BC at E. Prove that ∠ABC + ∠ACD = 2 ∠AEC.

121 Views

82. The sides BA and DC of a quadrilateral ABCD are produced as shown in figure. Show that ∠x + ∠y = ∠a + ∠b

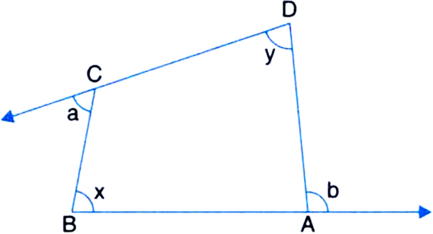
Given: The sides BA and DC of a quadrilateral ABCD are produced.
To Prove: ∠x + ∠y = ∠a + ∠b
Construction: Join BD

Proof: In ∆BCD,

∠a = ∠2 + ∠4 ...(1)
| Exterior angle theorem
In ∆ADB,
∠b = ∠1 + ∠3 ...(2)
| Exterior angle theorem
Adding (1) and (2), we get
∠a + ∠b = (∠1 + ∠2) + (∠3 + ∠4)
⇒ ∠a + ∠b - ∠x + ∠y

3484 Views

83. The degree measures of three angles of a triangle are x, y and z. If

straight z equals fraction numerator straight x plus straight y over denominator 2 end fraction comma

then find the value of z.

105 Views

84.

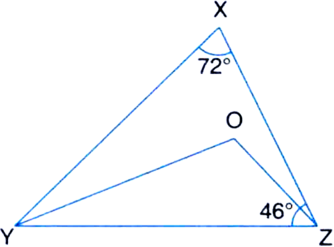
In figure, the sides AB and AC of ∆ABC are produced to points E and D respectively. If bisectors BO and CO of ∠CBE and ∠BCD respectively meet at point O, then prove that $angle BOC equals 90 degree minus 1 half angle BAC.$