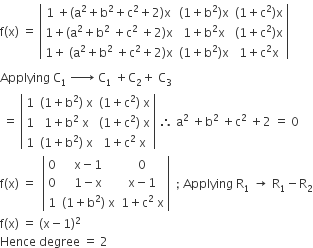Let A and B be two symmetric matrices of order 3.
Statement-1: A(BA) and (AB)A are symmetric matrices.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.

• Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is false. 

• Statement-1 is true, Statement-2 is false. 

The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is 

• less than 4

• 5

• 6

• 6

Let f : R → R be defined by

If f has a local minimum at x = - 1 then a possible value of k is

• 1

• 0

• -1/2

• -1/2

If S is the set of distinct values of 'b' for which the following system of linear equations
x + y + z = 1
x + ay + z = 1
ax + by + z = 0
has no solution, then S is

• a singleton

• an empty set

• an infinite set

• an infinite set

Let  ω be a complex number such that 2ω +1 = z where z = √-3. if


then k is equal to 

• 1

• -z

• z

• z

Let a, b, c be such that 0 (a +c) ≠ . If ,then the value of 'n' is 

• 0

• any even integer

• any odd integer

• any odd integer

Let A be a 2 × 2 matrix
Statement 1 : adj (adj A) = A
Statement 2 : |adj A| = |A|

• Statement–1 is true, Statement–2 is true, Statement–2 is a correct explanation for statement–1

• Statement–1 is true, Statement–2 is true; Statement–2 is not a correct explanation for statement–1.

• Statement–1 is true, statement–2 is false.

• Statement–1 is true, statement–2 is false.

If A and B are square matrices of size n × n such that A² − B² = (A − B) (A + B), then which of the following will be always true?

• A = B

• AB = BA

• either of A or B is a zero matrix

• either of A or B is a zero matrix

If A² – A + I = 0, then the inverse of A is

• A + I

• A

• A – I

• A – I

220.

If a² + b² + c² = -2 and  then f(x) is a polynomial of degree

• 1

• 0

• 2

• 2