Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas and hence that of the parllelogram. Does this agree with the formula that you know already?

526 Views

Short Answer Type

12.

Find the area the quadrilateral LMNOP (as shown in the figure).

949 Views

13. A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?

307 Views

14. Find the area of a rhombus whose diagonals are 12 cm and 9.2 cm.

335 Views

Long Answer Type

15. Find the area of these quadrilaterals:

289 Views

16. Divide the following polygons into parts (triangles and trapezium) to find out its area.

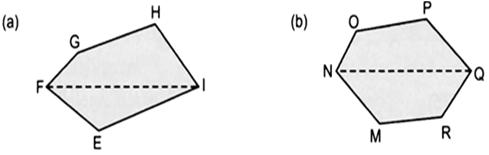
(a) We draw perpendiculars from opposite vertices on FI, i.e. $GL perpendicular space FI comma space space HM space perpendicular space FI space and space EN space perpendicular space FI$
Area of the polygon EFGHI
= $space space space space ar space left parenthesis straight capital delta space GFL right parenthesis space plus space ar space left parenthesis trapezium space GLMH right parenthesis space plus space ar space left parenthesis increment space HMI right parenthesis space plus space ar space left parenthesis increment space NEI right parenthesis space plus space ar space left parenthesis increment space EFN right parenthesis$
= $open parentheses 1 half FL space cross times space GL close parentheses space plus space 1 half space left parenthesis GL plus HM right parenthesis space cross times space LM space plus space open parentheses 1 half straight M 1 cross times MH close parentheses space plus space open parentheses 1 half straight N 1 cross times NE close parentheses space plus space open parentheses 1 half cross times FN cross times NE close parentheses$
 (a) We draw perpendiculars from opposite vertices on FI, i.e. ?

(b) NQ is a diagonal. Draw $OA perpendicular NQ comma space MB perpendicular space NQ comma space PC perpendicular space NQ space and space RD space perpendicular space NQ$

∴ Area of polygon OPQRMN = $ar space left parenthesis straight capital delta space OAN right parenthesis space plus space ar space left parenthesis trap. space CPOA right parenthesis plus space ar space left parenthesis straight capital delta space PCQ right parenthesis space plus space ar space left parenthesis straight capital delta space RDQ right parenthesis plus space ar space left parenthesis trap. space MBDR right parenthesis space plus space ar space left parenthesis straight capital delta space MBN right parenthesis$
= $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$
 $plus space open parentheses 1 half cross times CQ cross times PC close parentheses space plus space open parentheses 1 half cross times QD cross times RD close parentheses$
 $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

401 Views

17.

Polygon ABCDE is divided into parts as shown below. Find its area of AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.

Area of polygon ABCDE = Area of $straight capital delta space AFB$ + .........

Area of $increment space AFB$ = $1 half cross times AF cross times BF space equals space 1 half cross times 3 cross times 2 space equals space..........$

Area of trapezium FBCH = $FH cross times fraction numerator left parenthesis BF plus CH right parenthesis over denominator 2 end fraction$

= $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

Area of $increment space CHD space equals space$ $1 half cross times HD cross times CH space equals space........$

Area of $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$
So, the area of polygon ABCDE = ........

1661 Views

18.

Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2cm. NA, QC, QD and RB are perpendiculars to diagonal MP.

974 Views

Short Answer Type

19.

The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

203 Views

20. The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

604 Views