Short Answer Type
find out whether the following pair of linear equations are consistent, or inconsistent.
find out whether the following pair of linear equations are consistent, or inconsistent.
find out whether the following pair of linear equations are consistent, or inconsistent.
Long Answer TypeHalf the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Let the length of the garden be x m and width bey m.
Case I. x = y + 4
⇒ x - y = 4
Case II.
Half perimeter = 36
⇒ x + y =36
So algebraic representation be
x - y = 4
x + y = 36
Graphical representation :
We have, x - y = 4
⇒ x = 4 + y
Thus, we have following table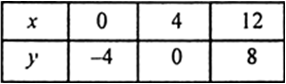
x + y = 36
⇒ x = 36 - y
Thus, we have following table :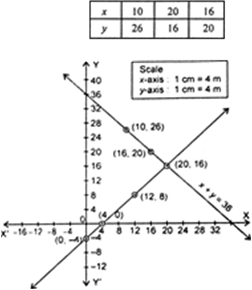
Fig. 3.10.
If we plot the graph of both the equations, we find that the two lines intersect at the point (20, 16). So, x = 20, y = 16 is the required solution of the given equation i.e., the length of the garden is 20 m and breadth be 16 m.
Short Answer TypeGiven the linear equations 2x + 3y - 8 = 0, write another linear equation in two variables such that the geometrical representing of the pair so formed is :
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Switch
