Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Pair of Linear Equations in Two Variables

Long Answer Type

191.

Draw the graph of the following equation x + y = 5, 3x - y = 3. Shade the region bounded by these lines and x-axis.

195 Views

192.

Nitish went to winter sale at Kamla Nagar to purchase some shirts and jackcts. When his friend asked him how many of each he had bought, he answered. “The number of jackets is three less than four times the number of shirts purchased. Also the number of jackets is four less than five times the numbers of shirts purchased.” Help his friends to find how many shirts and jackets Nitish bought. Express the solution graphically.

136 Views

193. Solve graphically the following system of linear equation, 2x + y = 6, x - 2y = -2. Also find the co-ordinates of the points where the lines meet the A-axis.

188 Views

194.

Represent the following pair of equations graphically and write the coordinates of points where the lines intersect y-axis :
x + 3y = 6
2x - 3y = 12

1918 Views

Short Answer Type

195. Solve the following system of equation by substitution method :

fraction numerator 3 straight x over denominator 2 end fraction minus fraction numerator 5 straight y over denominator 3 end fraction equals negative 2 straight x over 3 plus straight y over 2 equals 13 over 6

196 Views

196. Solve the following system of equation by substitution method :

square root of 2 straight x end root plus square root of 3 straight y end root equals 9 space space space space space space space space space space space square root of 3 straight x end root minus square root of 8 straight y end root equals 0 space space space space space space space space space space space

98 Views

197. A part of monthly expenses of a family is constant and the remaining varies with the price of wheat. When the rate of wheat is Rs. 250 a quintal, the total monthly expenses of the family are Rs. 1000 and when it is 240 a quintal, the total monthly expenses are Rs. 980. Find the total monthly expenses of the family when the cost of wheat is Rs. 350 a quintal.

1430 Views

198. A two digit number is obtained by either multiplying the sum of digits by 8 and adding 1 or by multiplying the difference of the digits by 13 and adding 2. Find the number.

Let the digit at 10’s place by x.
And, digit of unit’s place be y.
Then, Number = 10x + y
Case I. 10x + y = 8(x + y) + 1
⇒10x + y = 8x + 8y + 1
⇒    10x - 8x + y - 8y = 1
⇒    2x - 7y = 1
Case II.    10x + y = 13(x - y) + z
⇒    10x + y = 13x - 13y + 2
⇒ 10x - 13x + y + 13y = 2
⇒    -3x + 14y = 2
Thus, we have, 2x - 7y = 1    ...(i)
-3x + 14y = 2    ...(ii)
From (i), we have 2x - 7y = 1

$rightwards double arrow space space space space space space space space space space space space space space space space space space 2 x space equals space 7 y plus 1 rightwards double arrow space space space space space space space space space space space space x space equals space fraction numerator 7 y plus 1 over denominator 2 end fraction space space left parenthesis i i i right parenthesis$
Subtituting the value of (ii) and (iii), we get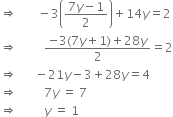

$rightwards double arrow space space space space space space space minus 3 open parentheses fraction numerator 7 y minus 1 over denominator 2 end fraction close parentheses plus 14 y equals 2 rightwards double arrow space space space space space space space space space fraction numerator negative 3 left parenthesis 7 y plus 1 right parenthesis plus 28 y over denominator 2 end fraction equals 2 rightwards double arrow space space space space space space minus 21 y minus 3 plus 28 y equals 4 rightwards double arrow space space space space space space space space space 7 y space equals space 7 rightwards double arrow space space space space space space space space space y space equals space 1$

Putting the value of y (iii), we get

$straight x equals fraction numerator 7 straight y plus 1 over denominator 2 end fraction equals fraction numerator 7 left parenthesis 1 right parenthesis plus 1 over denominator 2 end fraction equals fraction numerator 7 plus 1 over denominator 2 end fraction equals 8 over 2 equals 4$

Hence, Number = 10x + y
= 10(4) + 1 =4 0 + 1 = 41

568 Views

199. A and B are friends and their ages differ by 2 years. A’s father D is twice as old as A and B is hvicc as old as his sister C. The age of D and C differ by 40 years. Find the ages of A and B.

594 Views

200. A man sold a chair and a table together for Rs. 1520 thereby making a profit of 25% on the chair and 10% on table. By selling them together for Rs. 1535 he would have made a profit of 10% on the chair and 25% on the table. Find the cost price of each.

2448 Views