Let the cost price of one chair be Rs. x and that of one table be Rs. y. Profit on chair = 25%.

∴ Selling price of one chair 

Profit on a table = 10%

∴ Selling price of one table = 

According to the given condition, we have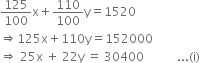

If profit on a chair is 10% and on a table is 25%, then total selling price is Rs. 1535.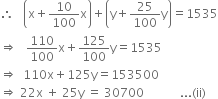

Subtracting equation (ii) from equation (i), we get
3x - 3y = -300 ⇒ x - y = -100
Adding equation (ii) and (i), we get
47x + 47y = 61100 ⇒ x + y = 1300
Thus, we have following equations
x - y = -100    ...(iii)
x + y = 1300    ...(iv)
From (iii), we have
x - y = - i 00
⇒    x = y - 100    ...(v)
Substituting the value of x in (iv), we get
x + y = 1300
⇒ y - 100 + y - 1300
2y - 100 = 1300
⇒    2y - 1400 ⇒ y = 700
Substituting the value of y in (v), we get
x = y - 100
⇒ x = 700 - 100 = 600
Hence, cost price of one chair = Rs. 600 and cost price of one table = Rs. 700