Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Pair of Linear Equations in Two Variables

Short Answer Type

201. Places A and B are 100 km. apart on a highway. On car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars ?

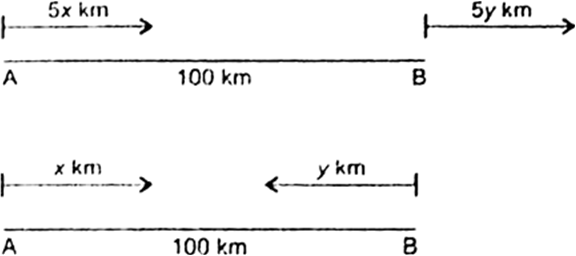
Fig. 3.26.
Let the speeds of two cars be x km./hr. and y km/hr.
Then, according to the given problem,
5x - 5y = 100
⇒ x - y = 20 ...(i)
and    x + y = 100 ...(ii)
By adding, we get    2x = 120
⇒    x = 60
By subtracting, we get 2y = 80
⇒    y = 40
Hence, the required speeds of the two cars are: 60 km/hr. and 40 km/hr.

303 Views

202. The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each saves Rs. 200 per month find their monthly incomes.

211 Views

203. A man travels 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and that of the car.

824 Views

204. The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?

248 Views

205.

Solve the following system of equations by elimination method

6(ax + by) = 3a + 2b
6(bx - ay) =3b - 2a.

606 Views

206. A man has only 20 paisc coins and 25 paise coins in his purse. If he has 50 coins in all, totalling Rs. 11.25. How many coins of each type does he share ? (Use Elimination Method).

225 Views

207. A person starts his job with a monthly income and earns a fixed increment every year. If his salary was Rs. 4500 after 4 years of service and Rs. 5400 after 10 years of service, find the initial salary and the annual increment by using elimination method.

655 Views

208.

A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32km upstream than to return downstream to the same spot. Find the speed of the stream.

3163 Views

Long Answer Type

209. A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?

1526 Views

210.

If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, then find the value of k.