Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Pair of Linear Equations in Two Variables

Short Answer Type

201. Places A and B are 100 km. apart on a highway. On car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars ?

303 Views

202. The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each saves Rs. 200 per month find their monthly incomes.

211 Views

203. A man travels 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and that of the car.

Let the speed of the train be x km/hr and that of the car be y km/hr.
We have following cases :
Case I. When he travels 250 km by train and the rest by car:
In this case, we have
Time taken by the man to travel 250 km by train

$equals 250 over straight x hrs$

Time taken by the man to travel (370 - 250)

$space space space space space space space space space equals 120 space km space by space car space equals space 120 over straight y hrs$
According to the given condition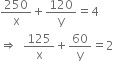

$250 over straight x plus 120 over straight y equals 4 rightwards double arrow space space 125 over straight x plus 60 over straight y equals 2$

Case II. When he travels 130 km by train and the rest by car:
Time taken by the man to travel 130 km by train

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

Time taken by the man to travel (370 - 130)

$equals space 240 space km space by space car space equals space 240 over straight y hrs$

According to the given condition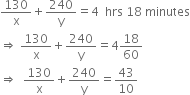

$130 over straight x plus 240 over straight y equals 4 space space hrs space 18 space minutes rightwards double arrow space 130 over straight x plus 240 over straight y equals 4 18 over 60 rightwards double arrow space space 130 over straight x plus 240 over straight y equals 43 over 10$

Thus, we have following system of equations :

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

$Putting space 1 over straight x equals straight u space and space 1 over straight y equals straight v comma space t h e space a b o v e space s y s t e m space r e d u c e s space t o$
125u + 60 v = 2 ....(i)

130u + 240v = $43 over 10 space space space space space space space space space space space space space space space space space.... left parenthesis ii right parenthesis$
Multiplying equation (iii) by 4 the above system of equations becomes

500u + 240v = 8 ...(iii)
130u + 240v = $space space space 43 over 10 space space space space space space space space space space space space... left parenthesis iv right parenthesis$
Subtracting equation (vi) from equation (iv), we get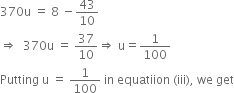

$370 straight u space equals space 8 space minus 43 over 10 rightwards double arrow space space 370 straight u space equals space 37 over 10 rightwards double arrow space straight u equals 1 over 100 Putting space straight u space equals space 1 over 100 space in space equatiion space left parenthesis iii right parenthesis comma space we space get$
5 + 240v = 8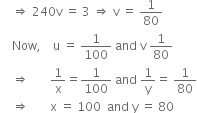
$space space space space space space rightwards double arrow space 240 straight v space equals space 3 space rightwards double arrow space straight v space equals space 1 over 80 space space space space Now comma space space space space straight u space equals space 1 over 100 space and space straight v space 1 over 80 space space space space rightwards double arrow space space space space space space space 1 over straight x equals 1 over 100 space and space 1 over straight y equals space 1 over 80 space space space space rightwards double arrow space space space space space space space straight x space equals space 100 space space and space straight y space equals space 80$

Hence, Speed of the train = 100 km/hr
Speed of the car = 80 km/hr.

824 Views

204. The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?

248 Views

205.

Solve the following system of equations by elimination method

6(ax + by) = 3a + 2b
6(bx - ay) =3b - 2a.

606 Views

206. A man has only 20 paisc coins and 25 paise coins in his purse. If he has 50 coins in all, totalling Rs. 11.25. How many coins of each type does he share ? (Use Elimination Method).

225 Views

207. A person starts his job with a monthly income and earns a fixed increment every year. If his salary was Rs. 4500 after 4 years of service and Rs. 5400 after 10 years of service, find the initial salary and the annual increment by using elimination method.

655 Views

208.

A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32km upstream than to return downstream to the same spot. Find the speed of the stream.

3163 Views

Long Answer Type

209. A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?

1526 Views

210.

If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, then find the value of k.