Short Answer Type
Long Answer TypeA class has 30 students. In how many ways can three prizes be awarded so that:
(a) no students get more than one prize?
(b) a student may get any number of prizes?
Short Answer TypeHow many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed.
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is not allowed.
Long Answer TypeShort Answer TypeDigits available are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Total number of digits = 10
Number of digits used = 3
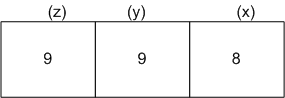
Number of filling box (z) = 9 [∴ If 0 is put in there, it becomes a two digit number]
m = 9
Number of ways of filling box (y) = 9 (3 Repetition is not allowed)
n = 9
Number of ways of filling box (x) = 8 (3 Repetition is not allowed)
p = 8
∴ The number of 3 digit numbers or numbers between 100 and 1000
= m x n x p = 9 x 9 x 8 = 648
Switch
