Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Permutations and Combinations

Short Answer Type

81. How many words can be formed by using the letters of the word ‘ORIENTAL’ so that A and E always occupy the odd places?

427 Views

82.

In how many ways can 5 girls be seated in a row so that two girls Ridhi and Sanya are:

(a) always together (b) never together

94 Views

83. How many different numbers of 6-digits can be formed by using digits 4,5,6,7,8,9 (a) no digit being repeated (b) digits may be repeated?

Also, find in case (a) as to how many of them arc odd, when repetition is not allowed?

85 Views

84. How many different numbers of 5-digit can be formed by using the digits 2,3, 4, 5 and 7, without repetition, so that the number is not divisible by 5?

96 Views

85. In how many ways can three prizes be given to 10 boys when a boy may receive any number of prizes?

101 Views

86. Find the number of 4-digit numbers in which any digit may be repeated any number of times.

90 Views

87. Find the number of 4-digit numbers in which no digit is repeated.

94 Views

88. Find the number of 4-digit numbers in which at least one digit is repeated.

93 Views

Long Answer Type

89. There are three prizes to be distributed among 6 students. In how many ways can this be done when

(a) no boy gets more than one prize.

(b) there is no restriction as to the number of prizes that a boy may get.

(c) no boy sets all prizes.

472 Views

90.
There are 8 students appearing for an examination, of which 3 appear in mathematics paper, and 5 in other different subjects. In how many ways can they be seated if

(a) all the students appearing for mathematics paper are together.

(b) the students appearing for mathematics paper are not all together.

(c) no two students appearing in mathematics paper are seated together ?

Step I: Tie the students appearing in mathematics paper together.

Number of permutations =

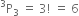
straight P presuperscript 3 subscript 3 space equals space 3 factorial space equals space 6

Mix the tie bundle with remaining 5 students to make 5 + 1 = 6.
Number of permutations =

straight P presuperscript 6 subscript 6 equals space space 6 factorial space equals space 720.

Hence, by fundamental principle of counting, the number of ways in which the students appearing in
mathematics paper sit together = 6 x 720 = 4320.

ALTERNATIVELY: n = 8, r = 3.

Number of permutations = r! (n- r + 1)! = 3! (8 - 3 + 1)! = 3! 6! = 6 x 720 = 4320.

(b) Total number of ways in which 8 boys may be seated without any condition

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

The number of ways in which the mathematics students are sitting together = 4320.
[By part (a)]
The number of ways in which the mathematics students are not all sitting together
= 40320 - 4320 = 36000

ALTERNATIVELY:

Number of permutations = n! - [r! (n - r + 1)!] = 8! - (3! 6!) = 36000

(C) When no two students appearing in mathematics paper are to sit together.

Arrange 5 remaining students by leaving one seat between every two students appearing in
examination other than mathematics.

Number of permutations =