 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeLet ![]() and
and ![]()
∵ ![]() are zeroes of p(x), then
are zeroes of p(x), then
![]() is a factor of p(x).
is a factor of p(x).
Now by applying division algorithm:
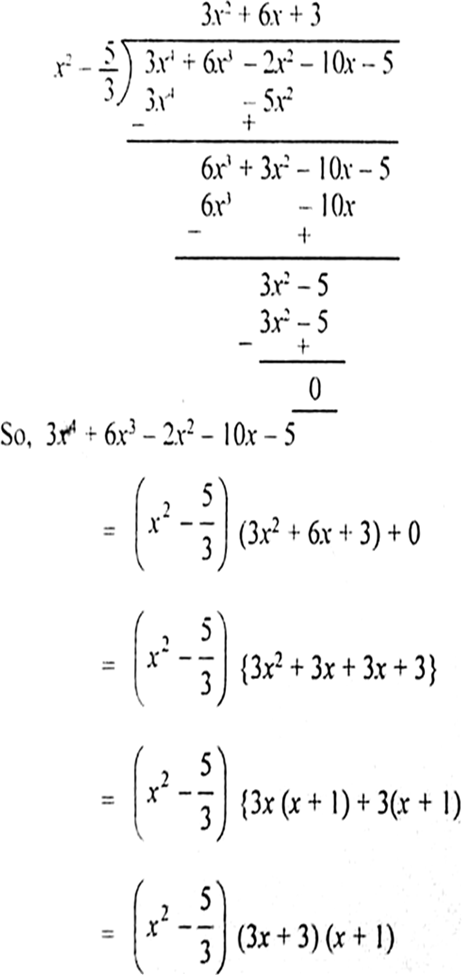
Therefore. the zeroes of the given fourth degree polynomial p(x) are
![]()
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type