Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

351. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and coefficients in each case:
x³ - 4x² + 5x - 2; 2, 1, 1

403 Views

Short Answer Type

352. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.

171 Views

Long Answer Type

353. If the zeroes of the polynomial x³ – 3x²+ x + 1 are (a – b), a, (a + b), find a and b.

226 Views

354. If two zeroes of the polynomial x⁴ – 26x³-26x² + 138x –35 are 2 ±

square root of 3

, find other two zeroes.

366 Views

355. If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² - 2x + k, the remainder comes out to be x + a, find ‘k’ and ‘a’.

By division algorithm, we have It is given that f(a) = x⁴ – 6x³ + 16x² – 25x + 10, when divided by x² – 2x + k leaves x + a as remainder.
:. f(x) – (x + a) = x⁴– 6x³ + 16x²–26x + 10 – a is is exactly divisible by x² – 2x + k.
Let us now divide x⁴ – 6x³ + 16x² – 26x + 10 – a by x² – 2x + k.
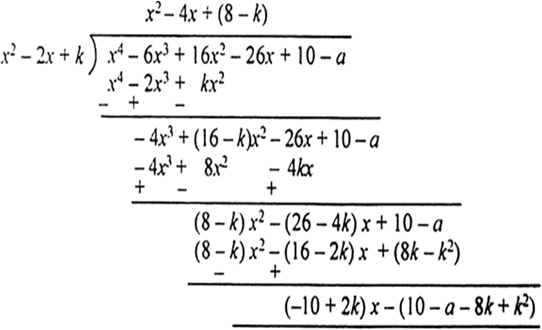
By division algorithm, we have It is given that f(a) = x4 – 6x3 +

By division algorithm, we have It is given that f(a) = x4 – 6x3 +

For f(x) – (x + a) = x⁴ – 6x³ + 16x² – 26x + 10 – a to be exactly divisible by x² – 2x + k, we must have
(–10 + 2k) x + (10 – a – 8k + k²) = 0 for all x
⇒ – 10 + 2k = 0, 10 – a – 8k + k² = 0
⇒ k = 5, 10 – a – 40 + 25 = 0
⇒ k = 5 and a = – 5.

2902 Views