Find all the zeros of the polynomial x4 + x3 – 34x2 – 4x
    • Zigya Logo

    Previous Year Papers

    Download Solved Question Papers Free for Offline Practice and view Solutions Online.

    Test Series

    Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

    Test Yourself

    Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.
    Advertisement

    Polynomials

    Multiple Choice QuestionsLong Answer Type

    431. If α, β are the zeroes of quadratic polynomial 2x2 – 3x – 5, form a quadratic polynomial whose zeroes are α2 and β2.
    397 Views
    Answer
    432. If α, β are the zeroes of quadratic poly-nomial x2 – 3x + 2, form a quadratic polynomial whose roots are –α and –β.
    161 Views
    Answer
    433. If α, β are the zeroes of quadratic polynomial x2 – 3x – 1, form a quadratic polynomial whose roots are 1 over straight alpha squared comma space 1 over straight beta squared.
    122 Views
    Answer
    434. Factorize 2x4 + x3 – 14x2 – 19x – 6 by x2 + 3x + 2 and verify the division algorithm.
    163 Views
    Answer
    Advertisement

    Multiple Choice QuestionsShort Answer Type

    435. Find all the zeroes of the polynomial x3 + 3x2 – 2x – 6, if two of its zeroes are – <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    1188 Views
    Answer
    436. Find all the zeroes of the polynomial 2a3 + x2 – 6x – 3, if two of its zeroes are - square root of 3 space and space square root of 3.
    230 Views
    Answer
    437. If the polynomial 6x4+8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2+ 4x +1, the remainder comes out to be (ax + b), find a and b.
    2132 Views
    Answer
    438. If the polynomial x3 + 2x3 + 8x2 + 12x + 18 is divided by another polynomial x2 + 5, the remainder comes out to be px + q. Find the values of p and q.
    211 Views
    Answer
    Advertisement

    Multiple Choice QuestionsLong Answer Type

    439. Find all the zeroes of 2x4 – 9x3 + 5x2 + 3x– 1, if two of its zeroes are 2 plus square root of 3 space and space 2 minus square root of 3.
    21071 Views
    Answer
    Advertisement
    Zigya App

    440. Find all the zeros of the polynomial x4 + x3 – 34x2 – 4x + 120, if two of its zeroes are 2 and (–2). 

    Since, two zeros are 2 and (–2),
    (x – 2) (x +2) = x2 – 4 is a factor of the given polynomial.
    Now, we divide the given polynomial by x2 – 4.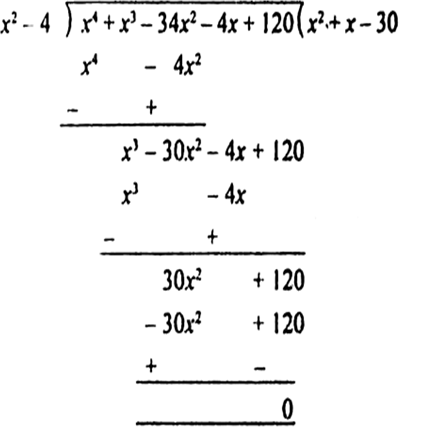
    Since, two zeros are 2 and (–2),(x – 2) (x +2) = x2 – 4 is a f
    ∴  straight x to the power of 4 plus straight x cubed minus 34 straight x squared minus 4 straight x plus 120 space equals space left parenthesis straight x squared minus 4 right parenthesis thin space left parenthesis straight x squared plus straight x minus 30 right parenthesis
    Now, x2 + x – 30 = x2 + 6x – 5x – 30
    = x (x + 6) – 5 (x + 6) = (x + 6)(x-5) So, its zeroes are given by x = – 6 and x = 5. Hence, the zeros of the given polynomial are : 2, (–2), (–6) and 5. 

    2997 Views
  • Switch Icon Switch
    • Advertisement
    Advertisement
    Flag Popup Icon
    Flag it
    Submit
    Flag Popup Icon
    Switch to
    flexipad
    Share It Icon
    Share it
    Share It
    Share it