Trying to find the right answer to this..

Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Polynomials

Short Answer Type

111. Find the value of k, if x - 1 is a factor of p(x) in each of the following cases:
p(x) = 2x²+ kx +

square root of 2

137 Views

112. Find the value of k, if x - 1 is a factor of p(x) in each of the following cases:

p(x) = kx² -

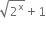
square root of 2 to the power of straight x end root plus 1

160 Views

113. Find the value of k, if x - 1 is a factor of p(x) in each of the following cases:

p(x)=kx² - 3x + k

234 Views

114. Factorise
12x² - 7x + 1

150 Views

115. Factorise
2x² + 7x + 3

130 Views

116. Factorise
6x² + 5x - 6

137 Views

117. Factorise
3x² - x - 4

117 Views

118. Factorise
x³ - 2x² - x + 2

x³ - 2x² - x + 2
Let p(x) = x³ - x² - x + 2
By trial, we find that
p(1) = (1)³ - 2(1)² - (1) + 2
= 1 - 2 - 1 + 2 = 0
∴ By Factor Theorem, (x - 1) is a factor of p(x).
Now,
x³ - 2x² - x + 2 = x²(x - 1) - x(x - 1) - 2(x - 1)
= (x - 1)(x² - x - 2)
= (x - 1)(x² - 2x + x - 2)
= (x - 1){x(x - 2) + 1(x - 2)}
= (x - 1)(x - 2)(x + 1).