Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Principle of Mathematical Induction

Long Answer Type

Use principle of mathematical induction to prove that:

$1 space plus space 2 space plus space 3 space plus space... space plus space straight n space equals space fraction numerator straight n left parenthesis straight n space plus space 1 right parenthesis over denominator 2 end fraction$

761 Views

Prove the following by using the principle of mathematical induction for all $straight n space element of space straight N colon$

$1 cubed plus 2 cubed plus 3 cubed plus space... space plus space straight n cubed space equals space open square brackets fraction numerator straight n left parenthesis straight n plus 1 right parenthesis over denominator 2 end fraction close square brackets squared$

596 Views

Prove the following by using the principle of mathematical induction for all $straight n element of straight N$ :

$1 plus 3 plus 3 squared plus....... space plus 3 to the power of straight n minus 1 end exponent space equals space fraction numerator 3 to the power of straight n minus 1 over denominator 2 end fraction$

398 Views

4.
Prove the following by using the principle of mathematical induction for all $straight n element of straight N$ :

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

Let P(n): $1 half plus space 1 fourth plus 1 over 8 plus....... plus 1 over 2 to the power of straight n space equals space 1 minus space 1 over 2 to the power of straight n$

I.    For n = 1,

     P(1) : $1 half space equals space 1 space minus space 1 over 2 to the power of 1 rightwards double arrow space 1 half space equals space 1 space minus space 1 half space space rightwards double arrow space 1 half space equals space 1 half$

∴    P(1) is true.

II.   Let the statement be true

       for n = m, $straight m space element of space straight N$

∴ $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$ .... (i)

III. For n = m + 1,

 P(m + 1): $1 half plus 1 fourth plus 1 over 8 plus......... plus 1 over 2 to the power of straight m plus 1 end exponent space equals space 1 space minus space 1 over 2 to the power of straight m plus 1 end exponent$

or $space space 1 half space plus space 1 fourth space plus space 1 over 8 space plus space......... space plus space 1 over 2 to the power of straight m plus 1 over 2 to the power of straight m plus 1 end exponent space equals space 1 space minus 1 over 2 to the power of straight m plus 1 end exponent$

 From (i),

 $1 half space plus space 1 fourth space plus space 1 over 8 space plus space.......... space plus space 1 over 2 to the power of straight m space equals space 1 space minus space 1 over 2 to the power of straight m$

∴   $straight P left parenthesis straight m plus 1 right parenthesis colon space 1 space minus space 1 over 2 to the power of straight m space plus space 1 over 2 to the power of straight m plus 1 end exponent space equals space 1 space minus space 1 over 2 to the power of straight m plus 1 end exponent$

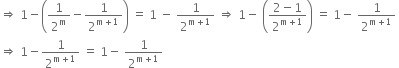
$rightwards double arrow space 1 minus open parentheses 1 over 2 to the power of straight m minus 1 over 2 to the power of straight m plus 1 end exponent close parentheses space equals space 1 space minus space 1 over 2 to the power of straight m plus 1 end exponent space rightwards double arrow space 1 minus space open parentheses fraction numerator 2 minus 1 over denominator 2 to the power of straight m plus 1 end exponent end fraction close parentheses space equals space 1 minus space 1 over 2 to the power of straight m plus 1 end exponent space rightwards double arrow space 1 minus 1 over 2 to the power of straight m plus 1 end exponent space equals space 1 minus space 1 over 2 to the power of straight m plus 1 end exponent$

      which is true.
∴    P(m + 1) is true
∴    P(m) is true $rightwards double arrow$ P(m + 1) is true

Hence, by the principal of mathematical induction, P(n) is true for all $straight n element of straight N$ .

376 Views

Prove the following by using the principle of mathematical induction for all $straight n element of straight N$ .

$fraction numerator 1 over denominator 3.5 end fraction space plus space fraction numerator 1 over denominator 5.7 end fraction space plus space fraction numerator 1 over denominator 7.9 space end fraction space plus space......... space plus space fraction numerator 1 over denominator left parenthesis 2 straight n plus 1 right parenthesis left parenthesis 2 straight n plus 3 right parenthesis end fraction space equals space fraction numerator straight n over denominator 3 space left parenthesis 2 straight n space plus space 3 right parenthesis end fraction$

329 Views

Prove the following by principle of mathematical induction for all $straight n element of straight N$ :

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$

226 Views

Prove the following by using the principle of mathematical induction for all $space space space space straight n element of straight N.$

$<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$ .

221 Views

Prove the following by using the principle of mathematical induction for all $space space straight n element of straight N.$

$1.3 space plus space 2.3 squared space plus space 3.3 cubed space plus space........ space plus space straight n.3 to the power of straight n space equals space fraction numerator left parenthesis 2 straight n minus 1 right parenthesis space 3 to the power of straight n plus 1 end exponent space plus space 3 over denominator 4 end fraction$

189 Views

Prove the following by using the principle of mathematical induction for all $straight n element of straight N colon$

$space space 1 plus fraction numerator 1 over denominator 1 plus 2 end fraction plus fraction numerator 1 over denominator 1 plus 2 plus 3 end fraction plus....... plus fraction numerator 1 over denominator 1 plus 2 plus 3 plus........ plus straight n end fraction space equals space fraction numerator 2 straight n over denominator straight n plus 1 end fraction$

173 Views

10.

Prove the following by using the principle of mathematical induction for all $space space straight n element of straight N.$

$1 plus 3 plus 5 plus........... space plus space left parenthesis 2 straight n minus 1 right parenthesis space equals space straight n squared$

276 Views

Previous Year Papers

Test Series

Test Yourself

Long Answer Type

4. Prove the following by using the principle of mathematical induction for all :