Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Probability

Fill In the Blanks

131. The probability of an event that cannot happen is ________ Such an event is called __________.

1001 Views

132. The probability of an event that is certain to happen is ________ Such an event is called _________.

928 Views

133. The sum of the probabilities of all the elemen-tary events of an experiment is ______.

641 Views

Short Answer Type

134. Which of the following arguments are correct and which are not correct ? Give reasons for your answer.

135. Two customers Shyam and Ekta are visiting a particular shop in the same weak (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on (i) the same day? (ii) consecutive days? (iii) different days?

342 Views

136. A die is a numbered in such a way that its face show the numbers 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws :

What is the probability that the total scene is (i) even, (ii) 6, (iii) at least 6.

118 Views

137. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of red ball, find the number of blue balls in the bag.

Number of red balls in the bag = 5 Let number of blue balls in the bag = x Total number of balls in the bag = x + 5 i.e., n(S) = x + 5
Let A be the favourable outcomes of getting red balls, then
n(A) = 5

Therefore, P(A) = $fraction numerator straight n left parenthesis straight A right parenthesis over denominator straight n left parenthesis straight S right parenthesis end fraction equals fraction numerator 5 over denominator x plus 5 end fraction$

Let B be the favourable outcomes of getting blue balls, then
n(B) = x

Therefore, P(B) = $fraction numerator straight n left parenthesis straight B right parenthesis over denominator straight n left parenthesis straight S right parenthesis end fraction equals fraction numerator x over denominator x plus 5 end fraction$

According to equation, P(B) = 2 P(A)

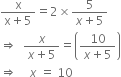
$rightwards double arrow$ $fraction numerator straight x over denominator straight x plus 5 end fraction equals 2 cross times fraction numerator 5 over denominator x plus 5 end fraction rightwards double arrow space space fraction numerator x over denominator x plus 5 end fraction equals open parentheses fraction numerator 10 over denominator x plus 5 end fraction close parentheses rightwards double arrow space space space space x space equals space 10$

Hence, the number of blue balls in the bag is 10.

625 Views

138.

A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.

367 Views

139. A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is

2 over 3

Find the number of blue balls in the jar.

2028 Views

140. A box contains cards marked with numbers 5 to 20. A card is drawn from the bag at random. Find the probability of getting a number which is a perfect square.

1116 Views