 Short Answer Type
Short Answer TypeA box contains 5 red balls, 4 green balls and 7 white balls. A ball is drawn at random from the box. Find the probability that the ball drawn is
(a) White (b) neither red nor white
Number of red balls in the box = 5
Number of green balls in the box = 4
Number of white balls in the box = 7
Total number of balls in the box = 16
i.e., n (S) = 16
(i) Let A be the favourable outcomes of getting white balls, then
n(A) = 7
Therefore,
P(A) = ![]()
(ii) Let B be the favourable outcomes of getting neither red nor white balls, then
n(B) = 1 - P (red or white)
= 1 - [P (red) + P (white)]
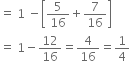
(i) white ball or a green ball.
(ii) neither a green ball not a red ball.
Cards marked with the numbers 2 to 101 are placed in a box and mixed throughly. One card is drawn from this box. Find the probability that the number on the cards is
(i) an even number
(ii) a number less than 14.
(iii) a number which is a perfect square.
(iv) a prime n umber less than 20.
18 Cards, numbered 1, 2, 3, ..., 18 are put in a box and mixed throughly. A card is drawn at random from the box. Find the probability that the Card drawn bears
(i) an even number
(ii) a number divisible by 2 or 3
12 cards, numbered 1, 2,3......., 12 are put in a box and mixed throughly. A card is drawn at random from the box. Find the probability that the card drawn bears
(i) an even number
(ii) a number divisible by 2 or 3.
