Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Probability

Short Answer Type

1061. An unbiased coin is tossed six times. Find the probability of obtaining at least 2 heads.

81 Views

1062. In a box containing 100 bulbs, 10 are defective. What is the probabilities that out of a sample of 5 bulbs
(i) none is defective (ii) exactly two are defective.

106 Views

1063. If “getting a 6” in a throw of an unbiased die is a success and the random variable x denotes the number of successes in five throws of the die, find P (2 < x < 5)

92 Views

1064. If “getting a 5 or a 6” in the throw of an unbiased die is a success and the random variable x denotes the number of successes in 6 throws of the die, find P (x ≤ 4).

97 Views

Long Answer Type

1065. A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the dice.

286 Views

Short Answer Type

1066. Eight coins are thrown simultaneously. Find the probability of getting at least six heads.

436 Views

Long Answer Type

1067.

A pair of dice is thrown 7 times. If getting a total of 7 is considered a success, what is the probability of
(i) no success? (ii) 6 successes? (iii) at least 6 successes? (iv) at most 6 successes?

128 Views

1068. Suppose X has a binomial distribution B

open parentheses 6 comma space 1 half close parentheses.

Show that X = 3 is the most likely outcome.

84 Views

1069. Find the mean of the Binomial distribution $straight B space open parentheses 4 comma space 1 third close parentheses.$

Let X be the random variable whose probability distribution is $straight B open parentheses 4 comma space 1 third close parentheses.$
$therefore space space straight n space equals space 4 comma space space space straight p space equals space 1 third space space and space straight q space equals space 1 minus 1 third space equals 2 over 3.$
Now $straight P left parenthesis straight X space equals straight x right parenthesis space equals space straight C presuperscript 4 subscript straight x space open parentheses 2 over 3 close parentheses to the power of 4 minus straight x end exponent space open parentheses 1 third close parentheses to the power of straight x comma space space space straight x space equals space 0 comma space 1 comma space 2 comma space 3 comma space 4.$
∴ the distribution of X is

$therefore$ mean = $sum from straight i space equals space 1 to 4 of straight x subscript straight i space straight p left parenthesis straight x subscript straight i right parenthesis space$
$equals space 0 space plus space straight C presuperscript 4 subscript 1 space open parentheses 2 over 3 close parentheses cubed space open parentheses 1 third close parentheses plus 2. space straight C presuperscript 4 subscript 2 space open parentheses 2 over 3 close parentheses squared space open parentheses 1 third close parentheses squared$
$plus 3. space space straight C presuperscript 4 subscript 3 space open parentheses 2 over 3 close parentheses space open parentheses 1 third close parentheses cubed plus 4 space straight C presuperscript 4 subscript 4 space open parentheses 1 third close parentheses to the power of 4$
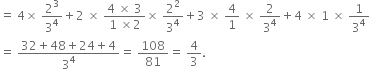
$equals space 4 cross times space 2 cubed over 3 to the power of 4 plus 2 space cross times space fraction numerator 4 space cross times space 3 over denominator 1 space cross times 2 end fraction cross times space 2 squared over 3 to the power of 4 plus 3 space cross times space 4 over 1 space cross times space 2 over 3 to the power of 4 plus 4 space cross times space 1 space cross times space 1 over 3 to the power of 4 equals space fraction numerator 32 plus 48 plus 24 plus 4 over denominator 3 to the power of 4 end fraction equals space 108 over 81 equals space 4 over 3.$