 Short Answer Type
Short Answer TypeProve that if E and F are independent events, then the events E and F' are also independent.
The random variable X can take only the values 0, 1, 2, 3. Given that P(X =0) = P(X = 1) = p and P(X = 2) = P(X = 3) such that Σpixi2 = 2Σpixi, find the value of p.
Often it is taken that a truthful person commands, more respect in the society. A man is known to speak the truth 4 out of 5 times. He throws a die and reports that it is a six.
Find the probability that it is actually a six.
Do you also agree that the value of truthfulness leads to more respect in the society?
Let H1 be the event that 6 appears on throwing a die
H2 be the event that 6 does not appear on throwing a die
E be the event that he reports it is six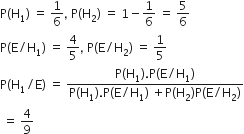
Yes ruthless leads to more respect in the society.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Two numbers are selected at random (without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X.
Suppose a girl throws a die. If she gets 1 or 2 she tosses a coin three times and notes the number of tails. If she gets 3,4,5 or 6, she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, what is the probability that she threw 3,4,5 or 6 with the ride ?
 Long Answer Type
Long Answer TypeA pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability distribution of the number of successes.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accident involving a scooter, a car and a truck are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.
Two groups are competing for the position on the Board of Directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product was introduced by the second group.
