 Multiple Choice Questions
Multiple Choice QuestionsIn a shop, there are five types of ice-creams available. A child buys six ice-creams.
Statement -1: The number of different ways the child can buy the six ice-creams is 10C5.
Statement -2: The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row.
Statement −1 is false, Statement −2 is true
Statement −1 is true, Statement −2 is true, Statement −2 is a correct explanation for Statement −1
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is
1/729
8/9
8/729
8/729
Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is
0.06
0.14
0.2
0.2
B.
0.14
The desired probability
= 0.7 × 0.2 + (0.7) (0.8) (0.7) (0.2) + (0.7) (0.8) (0.7) (0.8) (0.7) (0.2) + ….
= 0.14 [ 1 + (0.56) + (0.56)2 + … ]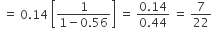
At a telephone enquiry system, the number of phone cells regarding relevant enquiry follow Poisson distribution with an average of 5 phone calls during 10-minute time intervals. The probability that there is at the most one phone call during a 10-minute time period is
6/5
5/6
6/55
6/55
Three houses are available in a locality. Three persons apply for the houses. Each applies to one house without consulting others. The probability that all the three apply for the same house is
2/9
1/9
8/9
8/9
A random variable X has Poisson distribution with mean 2. Then P(X > 1.5) equals
2/e2
0


Let x1, x2, …,xn be n observations such that  Then a possible value of n among the following is
Then a possible value of n among the following is
15
18
19
19
A random variable X has the probability distribution:
| X: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P(X): | 0.15 | 0.23 | 0.12 | 0.10 | 0.20 | 0.08 | 0.07 | 0.05 |
0.87
0.77
0.35
0.35
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 successes is
37/256
219/ 256
128/256
128/256
