Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Quadratic Equations

Long Answer Type

21. Find two consecutive positive integers, sum of whose square is 365.

143 Views

22. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm. Find the other two sides.

267 Views

Short Answer Type

23. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs. 90. Find the number of articles produced and the cost of each article.

200 Views

24. Find the roots of the following quadratic equations, if they exist by the method of completing the square:
2x² –7x + 3 = 0

213 Views

25. Find the roots of the following quadratic equations, if they exist by the method of completing the square:

2 straight x squared plus straight x minus 4 space equals space 0

117 Views

26. Find the roots of the following quadratic equations, if they exist by the method of completing the square:

4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0

106 Views

27. Find the roots of the following quadratic equations, if they exist by the method of completing the square:
2x²+x+ 4 = 0.

135 Views

Long Answer Type

28. Find the roots of the quadratic equations given in Q. 1, above by applying the quadratic formula.

(i) We have,
2x² – 1x + 3 = 0
Here, a = 2, b = –7 and c = 3
Now, b² – = (–7)² – 4(2) (3)
= 49 – 24 = 25 Since, b² – 4ac > 0
Therefore, the quadratic equation 2x² – 1x + 3 = 0 has distinct roots i.e. α and β.
Now, $<pre>uncaught exception: file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12 #0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...') #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...') #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #7 {main}</pre>$
$equals fraction numerator negative left parenthesis negative 7 right parenthesis plus-or-minus square root of 25 over denominator 2 cross times 2 end fraction equals fraction numerator 7 plus-or-minus 5 over denominator 4 end fraction$
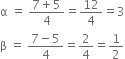
So, $straight alpha space equals space fraction numerator 7 plus 5 over denominator 4 end fraction equals 12 over 4 equals 3 straight beta space equals space fraction numerator 7 minus 5 over denominator 4 end fraction equals 2 over 4 equals 1 half$
Therefore, the required roots are 3 and $1 half.$

(ii) We have,
2x² + x – 4 = 0
Here, a = 2, b = 1 and c = –4
Now, b²– 4ac = (1)² –4 (2) (–4)
= 1 + 32 = 33
Since, b² – 4ac > 0
Therefore, the quadratic equation 2x² + x – 4 = 0 has distinct roots i.e. α and 946;.
Now, $<pre>uncaught exception: file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12 #0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...') #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...') #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #7 {main}</pre>$

 $equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 2 left parenthesis 2 right parenthesis end fraction equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 4 end fraction$

So, $straight alpha equals fraction numerator negative 1 plus square root of 33 over denominator 4 end fraction$
 $straight beta equals fraction numerator negative 1 minus square root of 33 over denominator 4 end fraction$

(iii) We have,
$4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0$
Here, $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$
Now, $straight b squared minus 4 ac space equals space left parenthesis 4 square root of 3 right parenthesis squared minus 4 space left parenthesis 4 right parenthesis space left parenthesis 3 right parenthesis$
 $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$
Since, $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$
Therefore, the quadratic equation $4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0$ has equal roots i.e. $straight alpha equals straight beta$
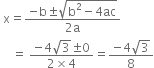
Now, $space straight x equals fraction numerator negative straight b plus-or-minus square root of straight b squared minus 4 ac end root over denominator 2 straight a end fraction space space space space equals space fraction numerator negative 4 square root of 3 plus-or-minus 0 over denominator 2 cross times 4 end fraction equals fraction numerator negative 4 square root of 3 over denominator 8 end fraction$
Therefore, the requried roots are $equals fraction numerator negative square root of 3 over denominator 2 end fraction.$

(iv) We have,
2x² + x + 4 = 0
Here, a = 2, b = 1 and c = 4
Now, b²– 4ac = (1)² – 4(2) (4)
= 1 – 32 = – 31
Since, b² – 4ac = 0
Therefore, the quadratic equation 2x² + x + 4 = 0 has no roots.

204 Views