Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Quadratic Equations

Long Answer Type

31. In a class, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product would have been 210. Find her marks in the two subjects.

157 Views

32. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.

211 Views

33. The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

185 Views

34. A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, would have taken 1 hour less for the same journey. Find the speed of the train.

1384 Views

35. Two water taps together can fill a tank in

space 9 3 over 8

hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

253 Views

36. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speed of the two trains.

261 Views

37. Sum of the area of the two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.

Let the side of first square = x m and the side of second square = y m
Then, the area of first square = x² m²and the area of second square = y² m²Perimeter of the first square = 4x m and perimeter of the second square = 4y m
Now, according to the given problem, we have x² + y² = 468 ...(i)
and 4x – 4y = 24
⇒ x – y = 6 ...(ii)
From equation (ii), we get
x – 6 + y = 0 ...(iii)
Putting this value of x in (i), we get
(6 + y)² + y²= 468 ⇒ 36+12y + f + y² = 468 ⇒ 2y²+ 12y + 36 – 468 =0
⇒ 2y² + 12y – 432 = 0
⇒ y² + 6y – 216 = 0 which is a quadratic equation in y.
We can solve this equation by quadratic formula.
Here, a = 1, b = 6, c = -216
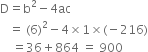
∴ $straight D equals straight b squared minus 4 ac space space space equals space left parenthesis 6 right parenthesis squared minus 4 cross times 1 cross times left parenthesis negative 216 right parenthesis space space space space equals 36 plus 864 space equals space 900$

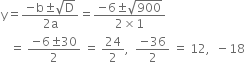
Now, $straight y equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator negative 6 plus-or-minus square root of 900 over denominator 2 cross times 1 end fraction space space space equals space fraction numerator negative 6 plus-or-minus 30 over denominator 2 end fraction space equals space 24 over 2 comma space space fraction numerator negative 36 over denominator 2 end fraction space equals space 12 comma space space minus 18$
But the side of a square cannot be -ve. y = 12 Putting this value of y in (iii), we get
x = 6 + 12 = 18 Hence, the side of the first square = 18 m and the side of the second square = 12 m. Ans.