Short Answer Type In a quadrilateral ABCD, the line segments bisecting ∠C and ∠D meet at E.
Prove that ∠A + ∠B = 2 ∠CED
ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram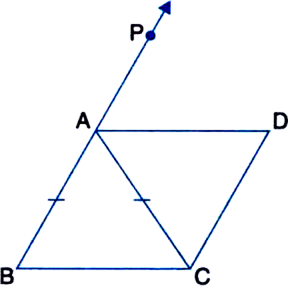
ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle ∠PAC and CD || AB (see figure). Show that:
(i) ∠DAC = ∠BCA and
(ii) ABCD is a parallelogram.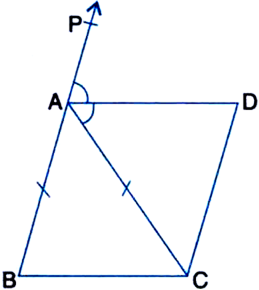
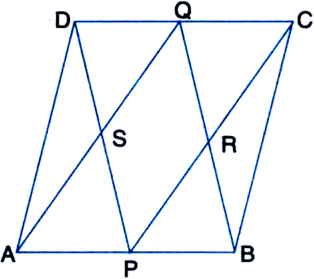
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.
