Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeDiagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.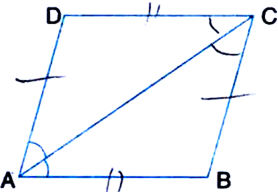
 Long Answer Type
Long Answer Type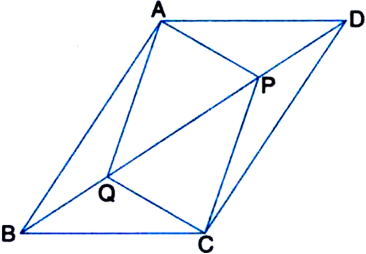
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ.
To Prove: (i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Construction: Join AC to intersect BD at O.
Proof: (i) In ∆APD and ∆CQB,
∵ AD || BC
| Opposite sides of parallelogram ABCD and a transversal BD intersects them
∴ ∠ADB = ∠CBD
| Alternate interior angles
⇒ ∠ADP = ∠CBQ ...(1)
DP = BQ | Given (2)
AD = CB ...(3)
| Opposite sides of ||gm ABCD In view of (1), (2) and (3)
∆APD ≅ ∆CQB
| SAS congruence criterion
(ii) ∵ ∆APD ≅ ∆CQB
| Proved in (i) above
∴ AP = CQ | C.P.C.T.
(iii) In ∆AQB and ∆CPD,
∵ AB || CD
| Opposite sides of ||gm ABCD and a transversal BD intersects them
∴ ∠ABD = ∠CDB
| Alternate interior angles
⇒ ∠ABQ = ∠CDP
QB = PD | Given
AB = CD
| Opp. sides of || gm ABCD
∴ ∆AQB ≅ ∆CPD | SAS Congruence Rule
(iv) ∵ ∆AQB = ∆CPD
| Proved in (iii) above
∴ AQ = CP | C.P.C.T.
(v) ∵ The diagonals of a parallelogram bisect each other.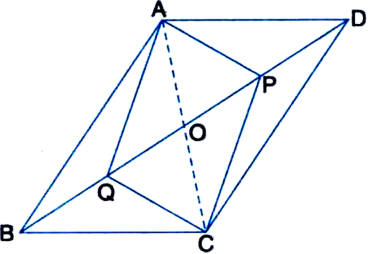
∴ OB = OD
∴ OB - BQ = OD - DP
| ∵ BQ = DP (given)
∴ OQ = OP ...(1)
Also, OA = OC ...(2)
| ∵ Diagonals of a || gm bisect each other
In view of (1) and (2), APCQ is a parallelogram.
 Short Answer Type
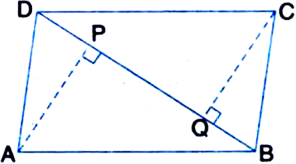
Short Answer TypeABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.