Short Answer Type
Long Answer TypeShort Answer TypeDiagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.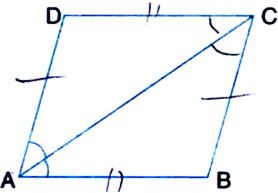
Long Answer Type
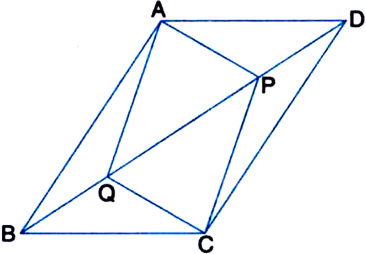
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Short Answer TypeABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.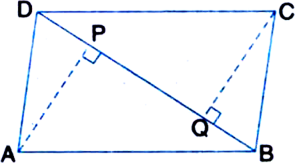
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively.
To Prove: (i) ∆APB ≅ ∆CQD
(ii) AP = CQ.
Proof: (i) In ∆APB and ∆CQD,
AB = CD
| Opp. sides of || gm ABCD
∠ABP = ∠CDQ
| ∵ AB || DC and transversal BD intersects them
∠APB = ∠CQD | Each = 90°
∆APB ≅ ∆CQD
| ∵ AAS Congruence Rule
(ii) ∵ ∆APB ≅ ∆CQD
| Proved above in (i)
∴ AP = CQ. | C.P.C.T.
Switch
