Long Answer TypeIn ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Short Answer TypeABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) diagonal AC = diagonal BD.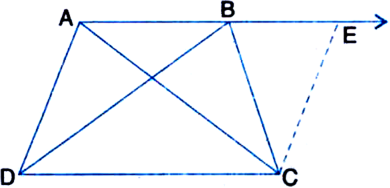
[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Long Answer TypeGiven: AB and CD are two parallel lines and a transversal I intersects AB at X and CD at Y.
To Prove: The bisectors of the interior angles form a rectangle.
Proof: ∵ AB || CD and EF intersects them
∴ ∠BXY = ∠CYX
| Alternate interior ∠s
| Halves of equals are equal
But these angles form a pair of equal alternate angles for lines XQ and SY and a transversal XY.
∴ XQ || SY ...(1)
Similarly, we can prove that
SX || YQ ...(2)
In view of (1) and (2),
SYQX is a parallelogram
| ∵ A quadrilateral is a parallelogram if both pairs of its opposite sides are parallel
Now, ∠BXY + ∠DYX = 180°
| Consecutive interior ∠s
⇒ ∠1 + ∠2 = 90°
But ∠1 + ∠2 + ∠XQY = 180°
| Angle sum property of a ∆
⇒ 90° + ∠XQY = 180°
⇒ ∠XQY = 90°
⇒ ∠YSX = 90°
| Opposite ∠s of a ||gm are equal
and ∠SXQ = 90°
| ∵ Consecutive interior angles on the same side of a transversal are supplementary
Now, ∠SXQ = 90°
⇒ ∠SYQ = 90°
| Opposite ∠s of a ||gm are equal
Thus each angle of the parallelogram SYQX is 90°. Hence parallelogram SYQX is a
rectangle.
Short Answer TypeLong Answer TypeShort Answer TypeGiven ∆ABC, lines are drawn through A, B and C parallel respectively to the sides
BC, CA and AB forming ∆PQR. Show that BC = 
Long Answer TypeABCD is a trapezium in which AB || CD and AD = BC. Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD.
Switch
