Long Answer TypeIn ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Short Answer TypeABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) diagonal AC = diagonal BD.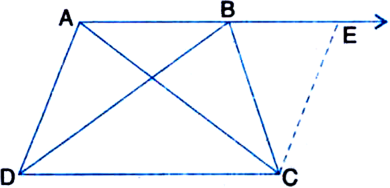
[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Long Answer TypeShort Answer TypeLong Answer TypeShort Answer TypeGiven ∆ABC, lines are drawn through A, B and C parallel respectively to the sides
BC, CA and AB forming ∆PQR. Show that BC = 
Long Answer TypeABCD is a trapezium in which AB || CD and AD = BC. Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD.
Given: ABCD is a trapezium in which AB || CD and AD = BC
To Prove:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD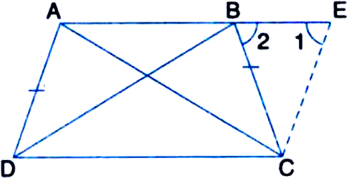
Construction: Through C, draw CE || DA to intersect AB produced at E.
Proof:
(i) ∵ AB || CD | Given
and AD || CE | by construction
∴ AECD is a parallelogram
| A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
∴ AD = EC
| Opposite sides of a parallelogram are equal
But AD = BC | Given
∴ BC = EC
∴ ∠1 = ∠2
| Angles opposite to equal sides of a triangle are equal
∠B + ∠2 = 180° ...(1)
| Linear Pair Axiom
∵ AD || EC | by construction
and AE intersects them
∴ ∠A + ∠1 = 180° ...(2)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
From (1) and (2),
∠B + ∠2 = ∠A + ∠1
But ∠1 = ∠2 | Proved above
∴ ∠B = ∠A
⇒ ∠A = ∠B
(ii) ∵ AB || DC | Given
and AD is a transversal
∴∠A + ∠D = 180° ...(3)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
∵ AB || DC | Given
and BC is a transversal.
∴ ∠B + ∠C = 180° ...(4)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
From (3) and (4),
∠A + ∠D = ∠B + ∠C
But ∠A = ∠B | Proved in (i
∴ ∠D = ∠C
⇒ ∠C = ∠D.
(iii) In ∆ABC and ∆BAD,
AB = BA | Common
BC = AD | Given
∠ABC = ∠BAD | Proved in (i)
∴ ∆ABC ≅ ∆BAD
| SAS congruence criterion
Switch
