Short Answer Type
Short Answer Type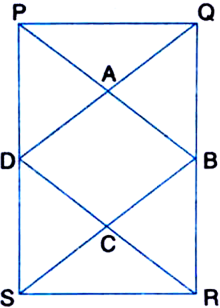
The angles A, B, C and D of a quadrilateral have measures in the ratio 2 : 4 : 5 : 7. Find the measures of these angles. What type of quadrilateral is it? Give reasons.
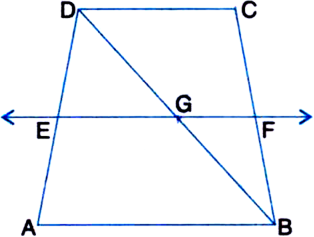
In the figure, ABCD is a parallelogram in which AB is produced to E so that AB = BE
(a) Prove that ED bisects BC
(b) If AD = 10 cm, find OB.
 Long Answer Type
Long Answer Type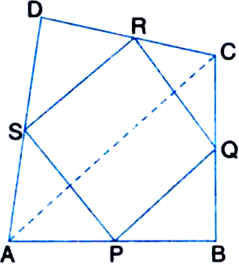
 Short Answer Type
Short Answer Type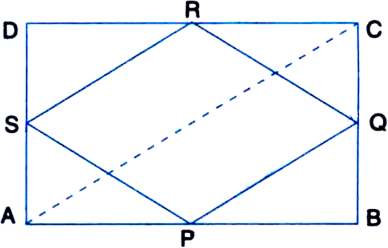
To Prove: Quadrilateral PQRS is a rhombus.
Construction: Join AC.
Proof: In ∆ABC,![]() P and Q are the mid-points of AB and BC respectively.
P and Q are the mid-points of AB and BC respectively.![]()
In ![]()
![]() S and R are the mid-points of AD and DC respectively.
S and R are the mid-points of AD and DC respectively.![]()
From (1) and (2),![]()
![]() Quardrilateral PQRS is a parallelogram ....(3_
Quardrilateral PQRS is a parallelogram ....(3_
In rectangle ABCD,
AD = BC | Opposite sides![]()
| Halves of equals are equal![]() AS = BQ
AS = BQ
In ![]()
AP = BP
| ∵ P is the mid-point of AB
AS = BQ | Proved above
∠PAS = ∠PBQ | Each = 90°
∴ ∆APS ≅ ∆BPQ
| SAS Congruence Axiom
∴ PS = PQ ...(4) | C.P.C.T.
In view of (3) and (4), PQRS is a rhombus.