Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Quadrilaterals

Long Answer Type

41. In a parallelogram ABCD, E and Fare the mid-points of sides AB and CD respectively. (see figure). Show that the line segments AF and EC trisect the diagonal BD.

322 Views

42. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.

333 Views

43.

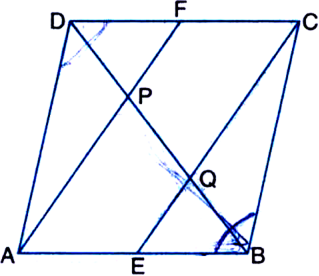
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:

(i) D is the mid-point of AC (ii) MD ⊥ AC (iii) $CM space equals space MA space equals space 1 half AB.$

443 Views

Short Answer Type

44. In triangle ABC, points M and N on sides AB and AC respectively are taken so that

AM equals 1 fourth AB space and space AN equals 1 fourth AC comma space

Prove that MN =

1 fourth

113 Views

45. In triangle ABC, points M and N on sides AB and AC respectively are taken so that

AM equals 1 fourth AB space and space AN equals 1 fourth AC comma space Prove space that space MN equals 1 fourth

280 Views

46. ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF. Prove that ED and FC are perpendicular to each other.

1943 Views

Long Answer Type

47. In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced to meet AC in F. Prove that $AF equals 1 third AC$

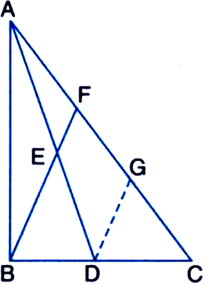
Given: In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced to meet AC in F.

To Prove: AF=

1 third

AC
Construction: Draw DG || EF to intersect AC in G.

Given: In ∆ABC, AD is the median through A and E is the mid-point o

Proof: ∵ EF || DG    | by construction
and    AE = ED
| ∵ E is the mid-point of AD
∴ AF = FG    ...(1)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
Again,
DG || EF    | by construction
and    CD = DB
| ∵ D is the mid-point of
∴ BC FG = GC    ...(2)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
From (1) and (2),
AF = FG = GC
Now, AF + FG + GC = AC
⇒ AF + AF + AF = AC
| From (1) and (2)
⇒ 3 AF = AC

rightwards double arrow space space AF equals 1 third AC

203 Views

48.

D, E, F are respectively the midpoints of the sides BC, CA and AB of a triangle ABC. Show that:
(i) BDEF is a parallelogram
(ii) DFEC is a parallelogram.

470 Views

Short Answer Type

49. In the figure ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F. Prove that AF = 2AB.

233 Views

Long Answer Type

50. ABCD is a trapezium in which side AB is parallel to the side DC and E is the mid-point of side AD (see figure). If F is a point on the side BC such that the segment EF is parallel to the side DC, prove that F is the mid-point of BC and EF =

1 half

(AB + DC).

5399 Views