 Long Answer Type
Long Answer Type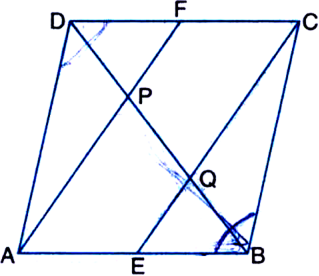
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the mid-point of AC (ii) MD ⊥ AC (iii) ![]()
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeD, E, F are respectively the midpoints of the sides BC, CA and AB of a triangle ABC. Show that:
(i) BDEF is a parallelogram
(ii) DFEC is a parallelogram.
 Short Answer Type
Short Answer Type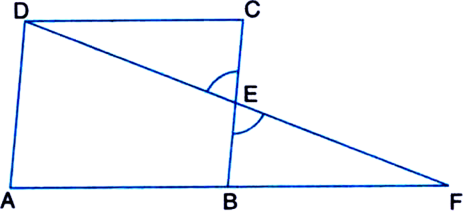
 Long Answer Type
Long Answer Type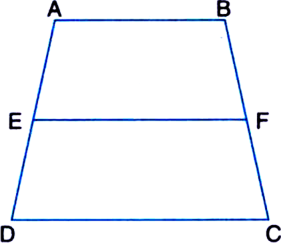
Given: ABCD is a trapezium in which side AB is parallel to the side DC and E is the mid-point of side AD. F is a point on the side BC such that the segment EF is parallel to the side DC.
To Prove: F is the mid-point of BC
and ![]()
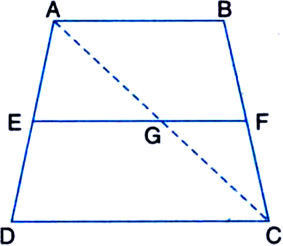
Construction: Join AC to intersect EF at G.
Proof:
(i) In ∆ADC,
∵ E is the mid-point of AD and
EG || DC | ∵ EF || DC
∴ G is the mid-point of AC
| by converse of mid-point theorem Again, In ∆CAB,
∵ G is the mid-point of AC | proved above
and GF || DC | ∵ EF || DC
∴ F is the mid-point of BC | by converse of
mid-point theorem
(ii) We shall prove that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and half of it.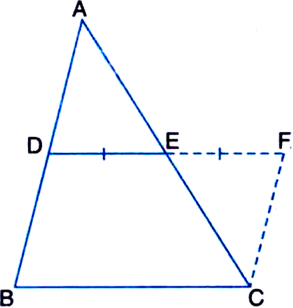
Let ABC be a triangle in which D and E are the mid-points of the sides AB and AC respectively.
We produce DE to F such that DE = EF and join FC.
In ∆AED and ∆CEF,
AE = CE
| ∵ E is the mid-point of AC
∠AED = ∠CEF
| Vertically opposite angles
ED = EF | by construction
∴ ∆AED ≅ ∆CEF
| SAS congruence rule
∴ AD = CF |CPCT
and ∠ADE = ∠CFE | CPCT
Now, ∵ D is the mid-point of AB
∴ AD = DB
But AD = CF | Proved above
∴ DB = CF ...(1)
Again, ∵ DF intersects AD and FC such that
∠ADE = ∠CFE | Proved above
But these angles form a pair of equal alternate interior angles
∴ AD || FC
⇒ DB || FC ...(2)
In view of (1) and (2),
DBCF is a parallelogram
| A quadrilateral is a parallelogram if one pair of its opposite sides is parallel and equal
∴ DF = BC
| Opposite sides of a parallelogram are equal
⇒ 2DE = BC | by construction![]()
Also, ∵ DBCF is a parallelogram
∴ DF || BC
| Opposite sides of a parallelogram are parallel
⇒ DE || BC
(iii) Using this result in ∆ADC,![]()
| ∵ E is the mid-point of AD and G is the mid-point of AC
and in ∆CAB,![]()
| ∵ G is the mid-point of AC and F is the mid-point of BC
Adding (3) and (4), we get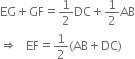
Also, EG || DC
⇒ EF || DC
