Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Quadrilaterals

Long Answer Type

51. ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that

CQ equals 1 fourth

AC (see figure). If PQ produced meets BC at R, prove that R is the mid-point of BC.

2180 Views

52. Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides.

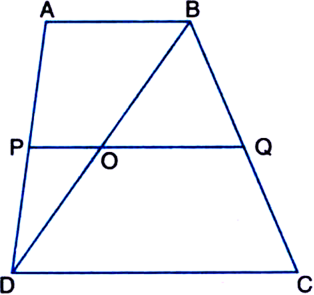
Given: ABCD is a trapezium. P and Q are the mid-points of the diagonals AC and BD respectively.
To Prove: PQ || AB
Construction: Join DP and produce so as to meet AB in R.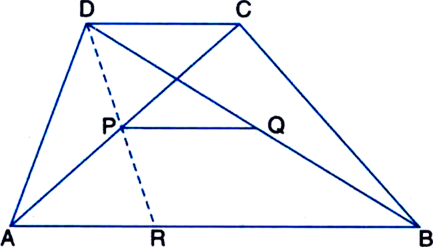

Proof: In ∆APR and ∆CPD,
∠PAR = ∠PCD
| Alternate interior angels [∵ AB || DC and a transversal AC intersects them]
∠APR = ∠CPD
| Vertically opposite angles
AP = CP    | Common
∴ ∆APR ≅ ∆CPD
| ASA congruence rule
∴ PR = PD    | CPCT
Now, in ∆DRB,
∵ P is the mid-point of DR | Proved above and Q is the mid-point of BD    |Given
∴ PQ || AB
Line segment joining the mid-points of any two sides of a triangle is parallel to the third side
But AB || DC
∴ PQ || AB || DC

196 Views

Short Answer Type

53. In ∆ABC, D, E and F are respectively the midpoints of sides AB, BC and CA (see figure). Show that ∆ABC is divided into four congruent triangles.

94 Views

54. I. m and n are three parallel lines intersected by transversals p and q such that I, m and n cut off equal intercepts AB and BC on p (see figure). Show that l, m and n cut off equal intercepts DE and EF on q also.

118 Views

55.

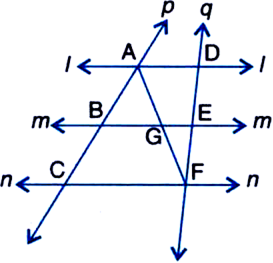
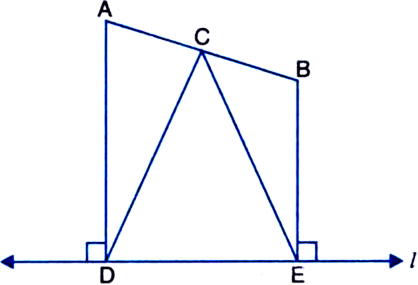
Points A and B are on the same side of a line l. AD and BE are perpendiculars to I, meeting at D and E respectively. C is the mid-point of AB. Prove that CD = CE
[Hint: From C draw the perpendicular CM on l.]

319 Views

56. In equilateral triangle ABC, the mid-points of the sides BC, CA and AB are respectively D, E and F as shown in the figure. Prove that DEF is also an equilateral triangle.

226 Views

57.

P is the mid-point of side AB of a parallelogram ABCD. A line through B parallel to PD meets DC at Q and AD produced at R (see figure). Prove that

(i) AR = 2 BC
(ii) BR = 2 BQ.

298 Views

58. In given figure ABCD is a trapezium in which AB || DC, BD is the diagonal and P is the mid- point of AD. A line is drawn through P, parallel to AB intersecting BC at Q. Show that CQ is equal to QB.

116 Views

59. In the figure, points A and B are on the same side of a line I. AD ⊥ l and BE ⊥ I at D and E respectively. If C is the mid-point of AB. prove that CD = CE.

104 Views

60. In ∆ABC, D, E and F are mid-points of sides AB, BC and CA. If AB = 6 cm, BC = 7.2 cm and AC = 7.8 cm, find the perimeter of ∆DEF.

224 Views