Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Real Numbers

Short Answer Type

21.

Prove that $square root of 5$ is irrational.

148 Views

22.
Prove that $space 3 plus 2 square root of 5$ is irrational.

Let us assume, to the contrary that

space 3 plus 2 square root of 5

is rational.

That is, we can find coprime a and b (b ≠ 0)

$such space that space space space space space space space space space space space 3 plus 2 square root of 5 equals straight a over straight b$

$Therefore comma space space straight a over straight b space equals space 3 space plus 2 square root of 5 space$

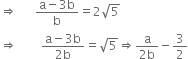
$rightwards double arrow space space space space space space fraction numerator straight a minus 3 straight b over denominator straight b end fraction equals 2 square root of 5 rightwards double arrow space space space space space space space space fraction numerator straight a minus 3 straight b over denominator 2 straight b end fraction equals square root of 5 rightwards double arrow fraction numerator straight a over denominator 2 straight b end fraction minus 3 over 2$

Since a and b are integers, we get $fraction numerator a over denominator 2 b end fraction minus 3 over 2$ is rational, and so $square root of 5$ is rational.

But this contradicts the fact that $square root of 5$ is irrational.

This contradiction has arisen because of our incorrect assumption that $space space space 3 plus 2 square root of 5$ is rational

So, we conclude that $space space 3 plus 2 square root of 5$ is irrational.

127 Views

23. Prove that the following are irrational:

(i)

fraction numerator 1 over denominator square root of 2 end fraction

94 Views

24. Prove that the following are irrational:

(ii)

7 square root of 5

95 Views

25. Prove that the following are irrational:

(iii)

6 plus square root of 2

113 Views

26.

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(i) $13 over 3125$

170 Views

27. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(ii)

17 over 8

102 Views

28. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

141 Views

29. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion: