Short Answer TypeIf 
be a rational number. Such that the prime factorisation ofq is not of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which is non-terminating repeating. Is this statement true ?
The following real numbers have decimal expansions as given below. In each case, Find whether they are rational or not.
(i) 43.123456789 (ii) 0.101001000 ....
Given integers are 4052 and 12576, clearly 12576 > 4052.
Therefore, by applying Euclid's division lemma to 4052 and 12576, we get
I. 12576 = 4052 × 3 + 420
II. Since the remainder 420 ≠ 0, we apply division lemma to 4052 and 420 to get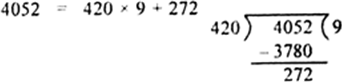
III. We consider the new divisor 420 and new remainder 272 and apply division lemma to gel 
IV. We consider the new divisor 272 and new remainder 148 and apply division lemma to get
V. We consider the new divisor 148 and new remainder 124 and apply division lemma to get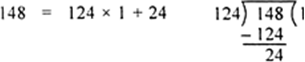
VI. We consider the new divisor 124 and new remainder 24 and apply division lemma to get
VII.We consider the new divisor 24 and new remainder 4 and apply division lemma to get
The remainder at this step is zero. So, the divisor at this stage or the remainder at the previous stage i.e. 4 is the HCF of 4052 and 12576.
Switch
