Short Answer TypeState whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a*a = a ∀ a ∈N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a.
Consider a binary operation * on N defined as a * b = a3 + b3 . Choose the correct answer.
(A) Is * both associative and commutative ?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Let A = Q x Q. Let be a binary operation on A defined by (a, b) * (c, d) = (ac, ad + b).
Then
(i) Find the identify element of (A, *)
(ii) Find the invertible elements of (A, *)
(i) Let (x, y) be the identify element of (A, *).
∴ (a, b) * (x,y) = (a, b) ∀ a, b ∈ Q ⇒ (ax, ay + b) = (a, b)
⇒ ax = a, ay + b = b ⇒ ax = a, ay = 0 ∀ a ∈ Q ⇒ x = 1, y = 0
Now (a, b) * (1,0) = (a, b) ∀ a, b, ∈ Q Also (1,0)* (a, b) = (a, 1. b + 0) = (a, b)
∴ (1, 0) is the identity element of A.
(ii) Let (a, b) ∈ A be invertible ∴ there exists (c, d) ∈ A such that (a, b) * (c, d) = (1, 0) = (c, d) * (a, b)
∴ (ac, ad + b) = ( 1,0) ⇒ ac = 1, ad + b = 0
Now a ≠ 0
∵ if a = 0, then (0, b) is not invertible as (0, b) invertible implies that here exists (c, d)∈ A such that (0, b) * (c, d) = (1, 0) or (0, b) = (1, 0), which is senseless.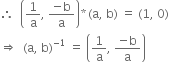
invertible elements of A are (a, b). a 
0 and (a, b)-1 = 
Define binary operation ‘*’ on Q as follows : a * b = a + b – ab, a, b∈ Q
(i) Find the identity element of (Q, *).
(ii) Which elements in (Q. *) are invertible?
is the inverse of a ≠ 0 for the multiplication operation ‘x’ on R.
Switch
