Short Answer TypeCheck the injectivity and surjectivity of the following functions:
f : N → N given by f(x) : x2Â
Check the injectivity and surjectivity of the following functions.
f : Z → Z given by f(x) = x2
Show that the Signum Function f : R → R, given by
           
is neither one-one nor onto
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
f : R → R defined by f(x) = 3 – 4x
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
f : R → R defined by f(x) = 1 + x2
f : R → R defined by
f(x) = 1 + x2
Let  
 such that 
 does not imply that x1 = x2 for instance
 f is not one-one
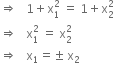
  f is not ontoConsider the binary operation A on the set {1, 2, 3, 4, 5} defined by a ∧ b = min. {a, b}. Write the operation table of the operation ∧.
Let A = Q x Q. Let be a binary operation on A defined by (a, b) * (c, d) = (ac, ad + b).
Then
(i) Find the identify element of (A, *)
(ii) Find the invertible elements of (A, *)
Switch
