Short Answer TypeThe pth, qth and rth terms of an A.P. are a, b, c respectively. Show that (q – r) a + (r – p) b + (p – q)c = 0
Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
How many terms of the A.P. -6, 
-5, .......... are needed to give the sum -25? Explain the double answer.
The given A.P. is: -6,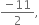 
-5, .............
Here, a = -6,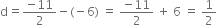 
Let -25 be the sum of n terms
∴ 
or 
or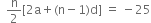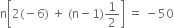 
or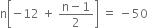 
or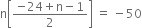 
or n(n - 25) = -100
or 
or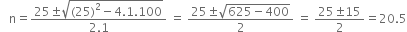 
Here, the common difference is positive.
∴ The A.P. starts from negative terms and its terms are increasing.
∴ All the terms after 13th term are positive.
These positive terms from 14th term to 20th term when added to negative terms from 6th term to 12th term, they cancel out each other and the sum remains same.
Hence, the sum of first five terms is same as the sum of first 20 terms.
In a A.P., the first term is 2 and the sum of first five terms is one-fourth of the sum of the next five terms. Show that the 20th term is – 112.
Long Answer TypeIf the sum of first n terms of a sequence is of the form An2 + Bw, where A and B arc constants (independent of n). Show that the sequence is an A.P. Is the converse true? Justify your answer.
Short Answer TypeIn an A.P., if the pth term is 
and the qth term is 
prove that the sum of the first pq terms must be 
where ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN11032647-3.png)
If the pth term of an A.P. is a and qth term is b, show that the sum of (p + q) terms
is 
Switch
