Short Answer TypeFind the sum of all natural numbers lying between 100 and 1000, which are mutliples of 5.
Find the sum of all the two digit numbers, which when divided by 4, yields 1 as remainder.
Find sum of integers from 1 to 100 that are divisible by 2 or 5.
Let 
= Sum of all the numbers from 1 to 100 which are divisible by 2.
= Sum of all the numbers from 1 to 100 which are divisible by 5.
= Sum of all numbers from 1 to 100 which are divisible by both 2 and 5.
∴ Required Sum =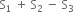 
...(i)
Now, 
Here, 
a + (n - 1)d = 1800 
2 + (n - 1)2 = 100
or (n - 1)2 = 98 or n - 1 = 
or n = 50
∴ 
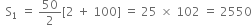
Here, a = 5, d = 5, 
a + (n - 1)d = 100 or 5 + (n - 1)5 = 100
n - 1 = 19 
n = 20
∴ 
∴ from (i), we have
Required sum = 2550 + 1050 - 550 = 3050.
<
The sum of first 4 terms of an A.P. is 56. The sum of last 4 terms is 112. If its first term is 11, then find the number of terms.
The sums of first n terms of two A.P.’s are in the ratio of 14 – 4n : 3n + 5. Find the ratio of their 8th terms.
The ratio of sums of m and n terms of an A.P. is m2 : n2. Show that the ratio of with and nth term is 2m – 1 :2n – 1.
Long Answer TypeIf S1, S2, S3 ........Sp are the sums of n terms of p A.P.’s whose first terms are 1, 2,3, .....p and common differences are 1, 3, 5, .....(2p – 1) respectively. Show that
Short Answer Type
Switch
