 Short Answer Type
Short Answer TypeIn a survey of 600 students, 150 were found to be drinking tea and 225 drinking coffee. 100 were drinking both tea and coffee. Find, how many students were neither drinking tea nor coffee?
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?
Let A = {a, b, c, d}, B = {b, c, d, e, f}, C = {b, c ,d, l, m}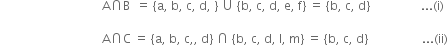
From (i) and (ii), we have
![]()
But, ![]()
Hence, ![]() need not imply B = C
need not imply B = C
Let A, B, and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. Show that B = C.
Show that for any sets A and B, A = ( A ∩ B ) ∪ ( A – B ) and A ∪ ( B – A ) = ( A ∪ B )
In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
In a group of 950 residents of a locality, every resident is fond of reading at least one of the morning newspapers published in English and Hindi. 750 of them like to read Hindi newspaper and 460 read the English newspapers. Find how many of them read
(i) Both the English newspaper and the Hindi newspaper.
(ii) English newspaper only.
(iii) Hindi newspaper only.
