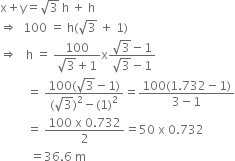Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Short Answer Type

21. From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°, Find the height of the tower.

1209 Views

22. In figure, what are the angles of depression from the positions O₁ and O₂ of the object at A?

1244 Views

23. The string of akite is 100 m long and its makes an angle of 60° with the horizontal. Find the height of the kite. Assume that there is no slackness in the string.

116 Views

24. In figure, what are the angles of depressions of the top and bottom of a pole from the top of a tower h m high.

120 Views

25. A balloon is connected to a meterological ground station by a cable length 215 m inclined at 60° to the horizontal determine the height of the baloon leave the ground. Assume that there is no slack in the cable.

116 Views

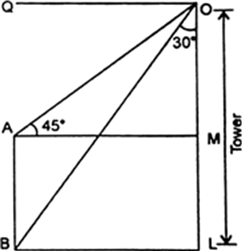
Long Answer Type

26. There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. A and B are points directly opposite to each other on two banks and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30° and 45°, find the length of the tree.

AQ = x m and BQ = y m and the angle of elevation of the top of the tree P from point A and B are 30° and 45° respectively.
i.e., ∠PAQ = 30° and ∠PBQ = 45°

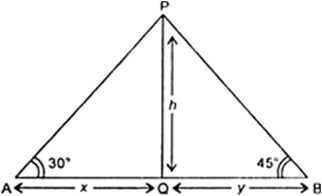
In right triangle
AQP, we have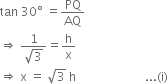

$tan space 30 degree space equals PQ over AQ rightwards double arrow space fraction numerator 1 over denominator square root of 3 end fraction equals straight h over straight x rightwards double arrow space straight x space equals space square root of 3 space straight h space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis straight i right parenthesis$
In right triangle BQP, we have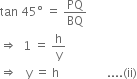

$tan space 45 degree space equals space PQ over BQ rightwards double arrow space space 1 space equals space straight h over straight y rightwards double arrow space space space straight y space equals space straight h space space space space space space space space space space space space space space space space.... left parenthesis ii right parenthesis$

Adding (i) and (ii), we get

$straight x plus straight y equals square root of 3 space straight h space plus space straight h rightwards double arrow space space 100 space equals space straight h left parenthesis square root of 3 space plus space 1 right parenthesis rightwards double arrow space space space straight h space equals space fraction numerator 100 over denominator square root of 3 plus 1 end fraction straight x fraction numerator square root of 3 minus 1 over denominator square root of 3 minus 1 end fraction space space space space space space space space space equals space fraction numerator 100 left parenthesis square root of 3 minus 1 right parenthesis over denominator left parenthesis square root of 3 right parenthesis squared minus left parenthesis 1 right parenthesis squared end fraction equals fraction numerator 100 left parenthesis 1.732 minus 1 right parenthesis over denominator 3 minus 1 end fraction space space space space space space space space space equals space fraction numerator 100 space straight x space 0.732 over denominator 2 end fraction equals 50 space straight x space 0.732 space space space space space space space space space space equals 36.6 space straight m$

753 Views

27. The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds the angle of elevation changes to 30°. If the jet plane is flying at a constant height of

bold 1500 square root of bold 3 bold space bold m

find the speed of the jet plane.

1899 Views

28. The angles of elevation of the top of a tower from two points at a distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is

square root of ab

metres.

4037 Views

29. An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.

1133 Views

30. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.

935 Views