Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Short Answer Type

21. From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°, Find the height of the tower.

1209 Views

22. In figure, what are the angles of depression from the positions O₁ and O₂ of the object at A?

1244 Views

23. The string of akite is 100 m long and its makes an angle of 60° with the horizontal. Find the height of the kite. Assume that there is no slackness in the string.

116 Views

24. In figure, what are the angles of depressions of the top and bottom of a pole from the top of a tower h m high.

120 Views

25. A balloon is connected to a meterological ground station by a cable length 215 m inclined at 60° to the horizontal determine the height of the baloon leave the ground. Assume that there is no slack in the cable.

116 Views

Long Answer Type

26. There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. A and B are points directly opposite to each other on two banks and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30° and 45°, find the length of the tree.

753 Views

27. The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds the angle of elevation changes to 30°. If the jet plane is flying at a constant height of

bold 1500 square root of bold 3 bold space bold m

find the speed of the jet plane.

1899 Views

28. The angles of elevation of the top of a tower from two points at a distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is $square root of ab$ metres.

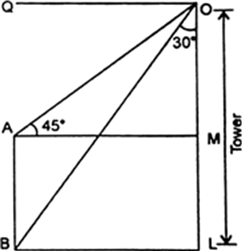
Let AB be the tower of height h metres, D and C are two points on the horizontal line, which are at distances a and b metres respectively from the base of the tower. It is also given that the angles of elevation of the top of a tower from two points D and C be complementary i.e.,
∠ADB = Ս then ∠ACB = (90 -ө)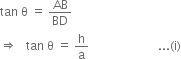

Let AB be the tower of height h metres, D and C are two points on the
In right triangle ADB, we have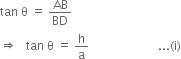

$tan space straight theta space equals space AB over BD rightwards double arrow space space space tan space straight theta space equals space straight h over straight a space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis straight i right parenthesis$
In right triangle ACB, we have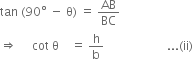

$tan space left parenthesis 90 degree space minus space straight theta right parenthesis space equals space AB over BC rightwards double arrow space space space space space cot space straight theta space space space space equals space straight h over straight b space space space space space space space space space space space space space space space space space space space space space... left parenthesis ii right parenthesis$
Multiplying (i) and (ii), we get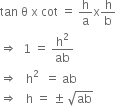

$tan space straight theta space straight x space cot space equals space straight h over straight a straight x straight h over straight b rightwards double arrow space space 1 space equals space straight h squared over ab rightwards double arrow space space space straight h squared space space equals space ab rightwards double arrow space space space straight h space equals space plus-or-minus space square root of ab$
But height can't be negative.

$apostrophe therefore space space space space space space space space space space space space space space straight h space equals space square root of ab$
Hence the height of the tower is $square root of ab space$ mts.

4037 Views

29. An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.

1133 Views

30. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.

935 Views