 Long Answer Type
Long Answer Type
Let CD be the flagstaff whose height is 7 m, fixed on the tower BC of height h metres. From a point A on the ground the angles of elevation of top and bottom of the flagstaff are 45° and 30° respectively.
In right triangle ABC, we have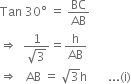
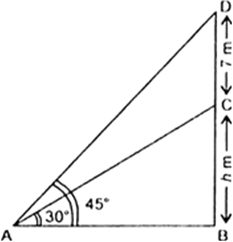
In right triangle ABD, we have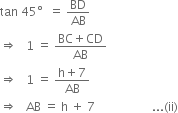
Comparing (i) and (ii), we get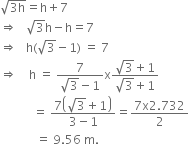
Hence, the height of the tower = 9.56 m.
 Short Answer Type
Short Answer Type