37. A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 metres away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and the width of the river. 

Let CD be the tree of height h m. Let B be the position of a man standing on the opposite bank of the river. After moving 40 m away from point B let new position of man be A i.e., AB = 40 m.
The angles of elevation of the top of the tree from point A and B are 30° and 60° respectively, i.e., ∠CAD = 30° and ∠CBD = 60°. Let BC = x m.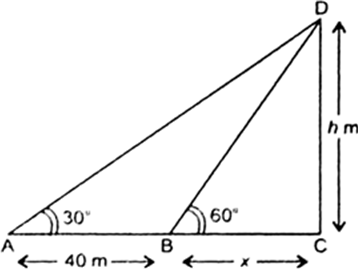


In right triangle BCD, we have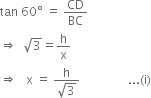


In right triangle ACD, we have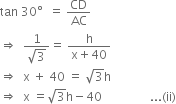


Comparing (i) and (ii), we get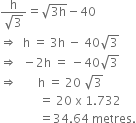


Hence, the height of the tree is 34.64 metres. Now substituting the value of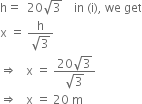


Hence, the width of the river is 20 m.