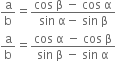45. A ladder rests against a wall at an angle α to the horizontal, its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. Show that  .

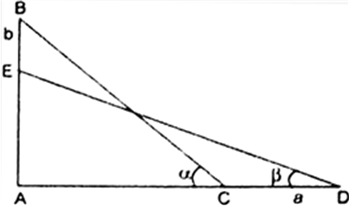
Let BC be the ladder which slides down a distance b on the wall.
In right triangle ABC, we have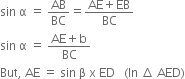



So, replacing AE by ED sin β, we get 

As, BC and ED both represent the same ladder.
BC = ED. (length of ladder does not change)
⇒ BC sin α - BC sin β = b
⇒ BC (sin α - sin β) = b    ...(i)
Similarly, in right triangle AED, we have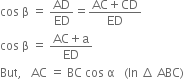


So, by replacing AC by BC cos α, we get ED cos β = BC cos α + a BC (cos . - cos α) = a [∴ ED = BC] ...(ii) Dividing (ii) by (i), we get