Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Short Answer Type

41. A round balloon of radius r subtends an angle α at the eye of the observer while the angle of elevation of its centre is β. Prove that the height of the centre of the balloon is r sin β . cosec α/2.

3368 Views

Long Answer Type

42. If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake be β. Prove that the distance of the cloud from the point of observer is

fraction numerator 2 straight h space sec space straight alpha over denominator tan space straight beta space minus space tan space straight alpha end fraction.

1314 Views

43. From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive stones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of aeroplane above the road is given by

fraction numerator tan space straight alpha space. space tan space straight beta over denominator tan space straight alpha space plus space tan space straight beta end fraction.

659 Views

44. From the top of a lighthouse the angle of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the lighthouse. Show that the distance

between the ship is

fraction numerator straight h left parenthesis tan space straight alpha space plus space tan space straight beta right parenthesis over denominator tan space straight alpha space minus space tan space straight beta end fraction

metres.

2168 Views

45. A ladder rests against a wall at an angle α to the horizontal, its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. Show that

straight a over straight b equals fraction numerator cos space straight alpha space minus space cos space straight beta over denominator sin space straight beta space minus space sin space straight alpha end fraction

574 Views

46. From a window h metres above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are ө and φ respectively. Show that the height of the opposite house is h ( 1 + tan ө. cot φ).

2122 Views

47. From the top of a tower the angles of depression of two objects on the same side of the tower are found to be α and β (α > β). If the distance between the objects is p metres,

show that the height It of the tower is given by h = $fraction numerator straight p space tan space straight alpha. space tan space straight beta over denominator tan space straight alpha space minus space tan space straight beta end fraction$ Also, determine the height of the tower if p = 50 metres, α = 60°, β = 30°.

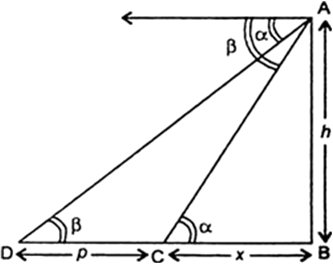
Case I : Let AB be the tower whose height is h metres. D arid C are the position of two objects which are p metres apart from each other. The angles of depression of two objects D and C from the top of the tower be β and α respectively.

i.e., ∠BDA = β and ∠BCA = α
In right triangle ABC, we have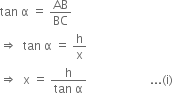

$tan space straight alpha space equals space AB over BC rightwards double arrow space space tan space straight alpha space equals space straight h over straight x rightwards double arrow space space straight x space equals space fraction numerator straight h over denominator tan space straight alpha end fraction space space space space space space space space space space space space space space space space space space space space space... left parenthesis straight i right parenthesis$
In right triangle ABD, we have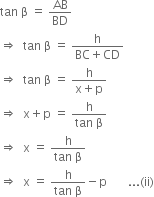

$tan space straight beta space equals space AB over BD rightwards double arrow space space tan space straight beta space equals space fraction numerator straight h over denominator BC plus CD end fraction rightwards double arrow space space tan space straight beta space equals space fraction numerator straight h over denominator straight x plus straight p end fraction rightwards double arrow space space straight x plus straight p space equals space fraction numerator straight h over denominator tan space straight beta end fraction rightwards double arrow space space straight x space equals space fraction numerator straight h over denominator tan space straight beta end fraction rightwards double arrow space space straight x space equals space fraction numerator straight h over denominator tan space straight beta end fraction minus straight p space space space space space space space... left parenthesis ii right parenthesis$
Comparing (i) and (ii), we get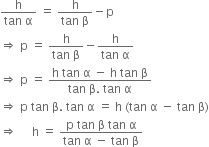

$fraction numerator straight h over denominator tan space straight alpha end fraction space equals space fraction numerator straight h over denominator tan space straight beta end fraction minus straight p rightwards double arrow space straight p space equals space fraction numerator straight h over denominator tan space straight beta end fraction minus fraction numerator straight h over denominator tan space straight alpha end fraction rightwards double arrow space straight p space equals space fraction numerator straight h space tan space straight alpha space minus space straight h space tan space straight beta over denominator tan space straight beta. space tan space straight alpha end fraction rightwards double arrow space straight p space tan space straight beta. space tan space straight alpha space equals space straight h space left parenthesis tan space straight alpha space minus space tan space straight beta right parenthesis rightwards double arrow space space space space space straight h space equals space fraction numerator straight p space tan space straight beta space tan space straight alpha over denominator tan space straight alpha space minus space tan space straight beta end fraction$
Case II : p = 50 m, α = 60°, β = 30°.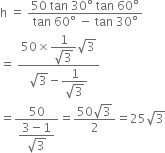

$straight h space equals space fraction numerator 50 space tan space 30 degree space tan space 60 degree over denominator tan space 60 degree space minus space tan space 30 degree end fraction equals space fraction numerator 50 cross times begin display style fraction numerator 1 over denominator square root of 3 end fraction end style square root of 3 over denominator square root of 3 minus begin display style fraction numerator 1 over denominator square root of 3 end fraction end style end fraction equals fraction numerator 50 over denominator begin display style fraction numerator 3 minus 1 over denominator square root of 3 end fraction end style end fraction equals fraction numerator 50 square root of 3 over denominator 2 end fraction equals 25 square root of 3$
= 20 x 1.732 = 43.25 m.
Hence, height of the tower is 43.25 m.

1906 Views

48. The angle of elevation of a cliff from a fixed point is ө. After going up a distance of K metres towards the top of the cliff at an angle of φ, it is found that the angle of elevation

is α. Show that the height of the cliff is

fraction numerator straight k left parenthesis cos space straight phi space minus space sin space straight phi. space cot space straight alpha right parenthesis over denominator cot space straight theta space minus space cot space straight alpha end fraction.

596 Views

49. Two stations due south of a leaning tower which leans towards the north are at distances a and b from its foot. If, α, β, are the elevations of the top of the tower from these stations,

prove that its inclination ө to the horizontal is given by cot

straight theta space equals space fraction numerator straight b space cot space straight phi space minus space straight a space cot space straight beta over denominator straight b space minus straight a space end fraction

783 Views

50. A pole 5 m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower.

155 Views