49. Two stations due south of a leaning tower which leans towards the north are at distances a and b from its foot. If, α, β, are the elevations of the top of the tower from these stations,

prove that its inclination ө to the horizontal is given by cot  

Let CE be the leaning tower. Let A and B be two given stations at distances a and b respectively from the foot of the tower.
Let CD = x and DE = h
In right triangle CDE, we have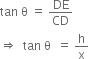




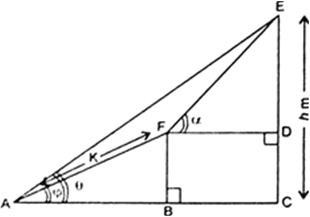
In right triangle BDE, we have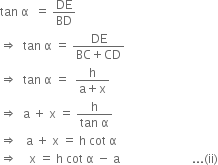


In right triangle ADE, we have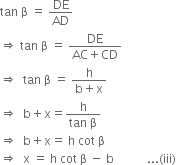


Comparing (i) and (ii), we get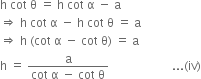



Comparing (i) and (iii), we get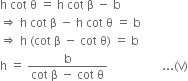



Comparing (iv) and (v), we get




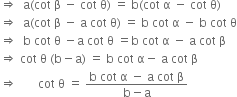
Hence, inclination ө to the horizontal is given by cot