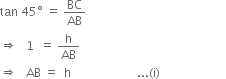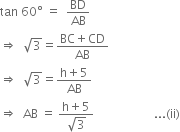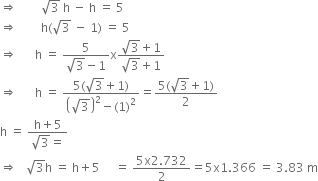50.
A pole 5 m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower.
Let BC be the height of the tower and CD be the pole of height 5m fixed on the top of the tower. Let BC = h m.

The angle of elevation of top of the pole from point A on the ground be 60° and the angle of depression of the point A from the top of the tower be 45°, i.e. ∠ BAD = 60° and ∠ BAC = 45°.
In right triangle ABC, we have
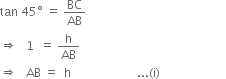
In right triangle ABD, we have
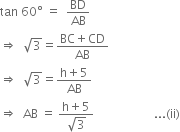 Comparing (i) and (ii), we get
Comparing (i) and (ii), we get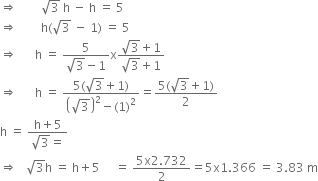
Hence, height of the tower be 6.83 m.
155 Views
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type