Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Long Answer Type

51. Two ships are sailing in the sea on the either side of the lighthouse, the angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200

open parentheses fraction numerator square root of 3 plus 1 over denominator square root of 3 end fraction close parentheses straight m.

Find the height of the lighthouse.

451 Views

52. A boy is standing on the ground and flying a kite with a string of length 150 m, at an angle of elevation of 30°. Another boy is standing on the roof of a 25 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string (in mts), correct to two decimal places, that the second boy must have so that the two kites meet.

372 Views

53. A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.

205 Views

54. At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is 5/12. On walking 192 metres towards the tower, the tangents of the angle is found to be 3/4. Find the height of the tower.

844 Views

55. The horizontal distance between two towers is 140 m. The angles of depression of the first tower, when seen from the top of the second tower is 30°. If the height of the first tower is 60 m. Find the height of the second tower.

710 Views

56. A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.

1761 Views

57. From the top of a building 100 m high, the angles of depression of the top and bottom of a tower are observed to be 45° and 60° respectively. Find the height of the tower. Also find the distance between the foot of the building and bottom of the tower.

5144 Views

58. The angles of depression of the top and bottom of an 8 m tall building from the top of a multistoreyed building are 30° and 45° respectively. Find the height of the multistoreyed building and the distance between the two buildings.

175 Views

59. There are two poles, one each on cither bank of a river, just opposite to each other. One pole is 60 m high. From the top of this pole, the angles of depression of the top and the foot of the other pole are 30° and 60° respectively. Find the width of the river and the height of the other pole.

695 Views

60. From the top and foot of a tower 40 m high, the angle of elevation of the top of a light house is found to be 30° and 60° respectively. Find the height of the lighthouse. Also find the distance of the top of the lighthouse from the foot of the tower.

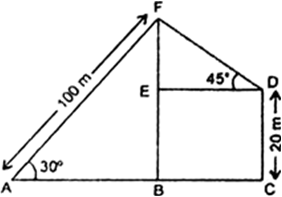
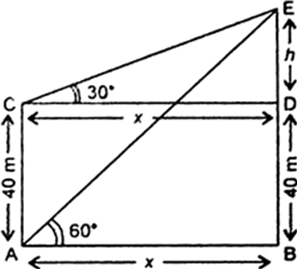
Let AC be the Tower such that AC = 40 m and BE be tine light house. Let CD be the horizontal from C. It is given that angles of elevation of the top of the light house from top and foot of the tower be 30° and 60° respectively.
i.e., ∠DCE = 30° and ∠BAE = 60°
Let AB = CD = x m and DE = x m
Now, in right triangle CDE, we have tan 30°

$equals space DE over CD rightwards double arrow space fraction numerator 1 over denominator square root of 3 end fraction equals straight h over straight x rightwards double arrow space space straight x space equals space square root of 3 straight h end root space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis straight i right parenthesis$
In right triangle ABE, we have

$tan space 60 degree space equals space BE over AB rightwards double arrow space space space space square root of 3 space equals space fraction numerator straight h plus 40 over denominator straight x end fraction rightwards double arrow space space space space straight x space equals space fraction numerator straight h plus 40 over denominator square root of 3 end fraction space space space space space space space space space space... left parenthesis ii right parenthesis$
Comparing (i) and (ii), we gel

$square root of 3 straight h end root space equals space fraction numerator straight h plus 40 over denominator square root of 3 end fraction rightwards double arrow space space space 3 straight h space equals space straight h space plus space 40 rightwards double arrow space space space 2 straight h space equals space 40 rightwards double arrow space space straight h space equals space 20 space straight m$

Hence,heighl of light house = BD + DE = 40 + 20 = 60 m.

In right triangle ABE, we have sin 60 $equals BE over AE$
$rightwards double arrow space space space fraction numerator square root of 3 over denominator 2 end fraction equals 60 over AE rightwards double arrow space space space space AE space equals space fraction numerator 120 over denominator square root of 3 end fraction rightwards double arrow space space space space AE space equals space fraction numerator 120 over denominator square root of 3 end fraction straight x fraction numerator square root of 3 over denominator square root of 3 end fraction equals 40 square root of 3 straight m$

Hence, the distance of the top of the light house from the foot of the tower is $40 square root of 3 space straight m$

3054 Views