Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Long Answer Type

61. A statue 1.46 m. tall stands on the top of a pedestal. From a point on the ground the angle of elevation of the top of statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45° find the height of the pedestal.

1868 Views

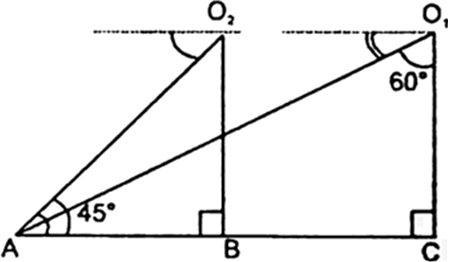
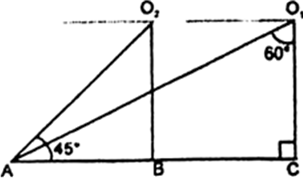
62. The angle of elevation of a jet fighter from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet is flying at a speed of 720 km/hour, find the constant height at which the jet is flying.

Let A be the point of observation, C and E be the two points of the plane. It is given that after 15 seconds angle of elevation changes from 60° to 30°.

i.e., ∠BAC = 60° and ∠DAE = 30°. It is also given that height of the jet plane is

1500 square root of 3 straight m.

straight i. straight e. space CB space equals space 1500 square root of 3

[Sincc jet plane is flying at constant height, Let, CB = ED = h km]
In right triangle ABC, we have

tan space 60 degree space equals space BC over AB rightwards double arrow space space square root of 3 space equals space straight h over AB rightwards double arrow space space space AB space equals space fraction numerator straight h over denominator square root of 3 end fraction space space space space space space space space space space space space space... left parenthesis straight i right parenthesis

In right triangle ADL, we have

tan space 30 degree space equals space DE over AD rightwards double arrow space fraction numerator 1 over denominator square root of 3 end fraction equals space fraction numerator DE over denominator AB plus BD end fraction rightwards double arrow space space fraction numerator 1 over denominator square root of 3 end fraction equals fraction numerator straight h over denominator AB plus BD end fraction rightwards double arrow space space space AB plus BD space equals space square root of 3 straight h rightwards double arrow space space space AB space equals square root of 3 straight h space minus space BD space space space space space space space space space space space space space space space space space space space space space... left parenthesis ii right parenthesis

Comparing (i) and (ii) we get,

fraction numerator straight h over denominator square root of 3 end fraction equals square root of 3 straight h minus BD rightwards double arrow space space BD space equals space square root of 3 straight h space minus fraction numerator straight h over denominator square root of 3 end fraction rightwards double arrow space space 3 space equals space fraction numerator 3 straight h minus straight h over denominator square root of 3 end fraction rightwards double arrow space space space 3 square root of 3 equals 2 straight h

[Hence, constant height at which the jet is flying = 2.6 km (app)]

BD space equals space 720 space straight x space fraction numerator 15 over denominator space 3600 end fraction equals 3 right square bracket rightwards double arrow space straight h space equals space fraction numerator 3 square root of 3 over denominator 2 end fraction rightwards double arrow space space straight h space equals space fraction numerator 3 cross times 1.732 over denominator 2 end fraction equals 2.598 rightwards double arrow space straight h space equals space 2.6 space km space left parenthesis approx right parenthesis

915 Views

63. A man on the deck of a ship 14 m above water level, observes that the angle of elevation of the top of a cliff is 60° and the angle of depression of the base of the cliff is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.

368 Views

Short Answer Type

64. The height of a tower is 10 m. Calculate the height of its shadow when Sun's altitude is 45°.

101 Views

65. In the following figure, what are the angles of depression from the observing positions O₁ and O₂ of the object at A?

96 Views

66. Find the angle of elevation of the Sun's altitude when the height of shadow of a vertical pole is equal to its height.

158 Views

67. In figure, what are the angles of depression of depression of the top and bottom of h m tall building from the top of multistoryed building.

150 Views

68.

From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°, Find the height of the tower.

102 Views

69. In figure, what are the angles of depression from the positions O₁ and O₂ of the object at A?

97 Views

70.

The string of akite is 100 m long and its makes an angle of 60° with the horizontal. Find the height of the kite. Assume that there is no slackness in the string.

146 Views